Dosya:Polynomialdeg3.svg - Vikipedi
İçeriğe atla
Ana menü
Gezinti
  • Anasayfa
  • Hakkımızda
  • İçindekiler
  • Rastgele madde
  • Seçkin içerik
  • Yakınımdakiler
Katılım
  • Deneme tahtası
  • Köy çeşmesi
  • Son değişiklikler
  • Dosya yükle
  • Topluluk portalı
  • Wikimedia dükkânı
  • Yardım
  • Özel sayfalar
Vikipedi Özgür Ansiklopedi
Ara
  • Bağış yapın
  • Hesap oluştur
  • Oturum aç
  • Bağış yapın
  • Hesap oluştur
  • Oturum aç

Dosya:Polynomialdeg3.svg

Sayfa içeriği diğer dillerde desteklenmemektedir.
  • Dosya
  • Tartışma
  • Oku
  • Wikimedia Commons üzerinde gör
  • Yerel açıklama ekle
  • Yerel açıklama kaynağı ekle
Araçlar
Eylemler
  • Oku
  • Wikimedia Commons üzerinde gör
  • Yerel açıklama ekle
  • Yerel açıklama kaynağı ekle
Genel
  • Sayfaya bağlantılar
  • Basılmaya uygun görünüm
  • Sayfa bilgisi
  • Kısaltılmış URL'yi al
  • Karekodu indir
Diğer projelerde
Görünüm
Vikipedi, özgür ansiklopedi
  • Dosya
  • Dosya geçmişi
  • Dosya kullanımı
  • Küresel dosya kullanımı
  • Üstveri
Dosya:Polynomialdeg3.svg
Bu SVG dosyasının PNG önizlemesinin boyutu: 400 × 400 piksel. Diğer çözünürlükler: 240 × 240 piksel | 480 × 480 piksel | 768 × 768 piksel | 1.024 × 1.024 piksel | 2.048 × 2.048 piksel.
Tam çözünürlük (SVG dosyası, sözde 400 × 400 piksel, dosya boyutu: 737 bayt)
Bu dosya Wikimedia Commons'ta bulunmaktadır. Dosyanın açıklaması aşağıda gösterilmiştir.
Commons, serbest/özgür telifli medya dosyalarının bulundurulduğu depodur. Siz de yardım edebilirsiniz.
Bu dosya Wikimedia Commons'ta bulunmaktadır.

Özet

AçıklamaPolynomialdeg3.svg

Polynomial of degree 3 with roots at 2, -1, and -4:

y = 1 4 ( x + 4 ) ( x + 1 ) ( x − 2 ) = 1 4 ( x 3 + 3 x 2 − 6 x − 8 ) = 1 4 x 3 + 3 4 x 2 − 3 2 x − 2 {\displaystyle {\begin{aligned}y&={\tfrac {1}{4}}(x+4)(x+1)(x-2)\\&={\tfrac {1}{4}}(x^{3}+3x^{2}-6x-8)\\&={\tfrac {1}{4}}x^{3}+{\tfrac {3}{4}}x^{2}-{\tfrac {3}{2}}x-2\end{aligned}}} {\displaystyle {\begin{aligned}y&={\tfrac {1}{4}}(x+4)(x+1)(x-2)\\&={\tfrac {1}{4}}(x^{3}+3x^{2}-6x-8)\\&={\tfrac {1}{4}}x^{3}+{\tfrac {3}{4}}x^{2}-{\tfrac {3}{2}}x-2\end{aligned}}}
Tarih 6 Ocak 2007
Kaynak Polynomialdeg3.png
Yazar N.Mori
İzin
(Bu dosyanın tekrar kullanımı)
Public domainPublic domainfalsefalse
Public domain Bu iş yazarı N.Mori tarafından kamu malı olarak yayınlanmıştır. Bu dünya çapında geçerlidir.
Bazı ülkelerde bu yasal olarak mümkün olmayabilir; öyleyse:
N.Mori, bu işi herhangi bir amaç için, herhangi bir şart olmaksızın, yasalarca gerekli olmadıkça, herkesin kullanmasına izin veriyor.
SVG gelişimi
InfoField
 Bu SVG kaynak kodu geçerlidir.
 Bu vektörel grafik Matplotlib ile oluşturuldu.
Kaynak kodu
InfoField

Python code

Source code 
# Author: Ika, 2013-07-24
from pylab import *
import pylab as pl
import numpy as np

# Create a figure of size 8x6 points, 80 dots per inch
pl.figure(figsize=(8,8), dpi=80)

# Create a plot of the cubic function y=(x+4)(x+1)(x-2)/4
x = np.linspace(-5.0,4.0,256, endpoint=True)
y = (x+4)*(x+1)*(x-2)/4
pl.plot(x,y,color="magenta", linewidth=3.0, linestyle="-")

# Set labels
pl.xlim(-5,4)
pl.ylim(-4,7)

# Move the spines
ax = pl.gca()
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.text(-5, 3, r'$y=\frac{1}{4}(x+4)(x+1)(x-2)$', fontsize=20)

# Set up the grid
ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none')
ax.xaxis.set_ticks_position('bottom')
ax.spines['bottom'].set_position(('data',0))
ax.yaxis.set_ticks_position('left')
ax.spines['left'].set_position(('data',0))
ax.grid(color="grey",linestyle='--',linewidth=1)

# Save the figure to the output SVG file
plt.savefig("Cubic_Function_SVG.svg");

Altyazılar

Bu dosyanın temsil ettiği şeyin tek satırlık açıklamasını ekleyin.
Graphing of a third degree polynomial, with roots at -4, -1 and 2, and a y-intercept of -2.
Graphe d'un polynôme de degré 3, avec des racines en -4, -1 et 2, et une ordonnée à l'origine en -2.

Bu dosyada gösterilen öğeler

betimlenen

plot İngilizce

denklem

telif hakkı durumu

copyrighted, dedicated to the public domain by copyright holder İngilizce

telif hakkı alınmış

telif hakkı lisansı

released into the public domain by the copyright holder İngilizce

kuruluşu

6 Ocak 2007

dosya boyutu

737 bayt

ortam türü

image/svg+xml

sağlama toplamı

6b25de438d8c38ccbc816cead66e0c79b7d47094

tespit yöntemi: SHA-1

Dosya geçmişi

Dosyanın herhangi bir zamandaki hâli için ilgili tarih/saat kısmına tıklayın.

Tarih/SaatKüçük resimBoyutlarKullanıcıYorum
güncel16.33, 2 Ocak 201516.33, 2 Ocak 2015 tarihindeki sürümün küçültülmüş hâli400 × 400 (737 bayt)KrishnavedalaReverted to version as of 13:02, 30 August 2008: Cleaner rendering. text and graph not clear in the newly uploaded version.
08.33, 24 Temmuz 201308.33, 24 Temmuz 2013 tarihindeki sürümün küçültülmüş hâli720 × 720 (34 KB)IkamusumeFan1. Redrew completely using Matplotlib; 2. Source code added; 3. Labels added.
13.02, 30 Ağustos 2008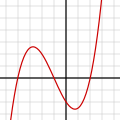13.02, 30 Ağustos 2008 tarihindeki sürümün küçültülmüş hâli400 × 400 (737 bayt)N.Mori{{Information |Description= |Source= |Date= |Author= |Permission= |other_versions= }}
13.42, 6 Ocak 2008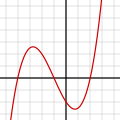13.42, 6 Ocak 2008 tarihindeki sürümün küçültülmüş hâli400 × 400 (965 bayt)N.Mori{{Information| |Description=Polynomial of degree 3: <math>y=\frac{x^3}{4}+\frac{3x^2}{4}-\frac{3x}{2}-2=\frac{1}{4}(x+4)(x+1)(x-2)</math> |Source=Image:Polynomialdeg3.png |Date=2007-01-06 |Author=~~~ |Permission=See below |other_versions=None }} [[Cat

Dosya kullanımı

Bu görüntü dosyasına bağlantısı olan sayfalar:

  • Cebir
  • Eğriler galerisi

Küresel dosya kullanımı

Aşağıdaki diğer vikiler bu dosyayı kullanmaktadır:

  • af.wikipedia.org üzerinde kullanımı
    • Derdegraadse vergelyking
  • am.wikipedia.org üzerinde kullanımı
    • ኩቢክ እኩልዮሽ
  • ar.wikipedia.org üzerinde kullanımı
    • الجبر
    • معادلة تكعيبية
    • متعددة الحدود
    • خواص جذور متعددة حدود
    • مستخدم:عبد المؤمن/مصور
    • دالة قابلة للاشتقاق
  • az.wikipedia.org üzerinde kullanımı
    • Çoxhədli
    • Kubik funksiya
    • Diferensiallanan funksiya
  • ba.wikipedia.org üzerinde kullanımı
    • Тигеҙләмә
  • be.wikipedia.org üzerinde kullanımı
    • Мнагачлен
  • bg.wikipedia.org üzerinde kullanımı
    • Алгебра
    • Кубично уравнение
  • bn.wikipedia.org üzerinde kullanımı
    • বীজগণিত
    • বহুপদী
    • ব্যবহারকারী:Milandeep Sarkar/বহুপদী
    • ত্রিঘাত সমীকরণ
    • ব্যবকলনযোগ্য ফাংশন
  • bo.wikipedia.org üzerinde kullanımı
    • ཚབ་རྩིས།
  • bs.wikipedia.org üzerinde kullanımı
    • Kubna funkcija
  • ca.wikipedia.org üzerinde kullanımı
    • Funció derivable
    • Funció cúbica
    • Usuari:AMontes/proves
    • Usuari:AMontes/Polinomi
    • Usuari:AMontes/proves/Proves de Polinomi
  • ckb.wikipedia.org üzerinde kullanımı
    • ڕادەدار
  • cv.wikipedia.org üzerinde kullanımı
    • Яка функци
    • Дифференциленекен функци
  • cy.wikipedia.org üzerinde kullanımı
    • Algebra
    • Polynomial
  • de.wikipedia.org üzerinde kullanımı
    • Differenzierbarkeit
    • Ganzrationale Funktion
  • de.wikiversity.org üzerinde kullanımı
    • Kurs:Maßtheorie auf topologischen Räumen/Differenzierbarkeit in Analysis und Funktiontheorie
  • el.wikipedia.org üzerinde kullanımı
    • Άλγεβρα
    • Πολυώνυμο
    • Χρήστης:Mkpapager/Πρόχειρο
  • en.wikipedia.org üzerinde kullanımı
    • Polynomial
    • Cubic equation
    • Cubic function
    • Differentiable function
    • Gallery of curves
    • User:Ramzuiv/sandbox
    • User:Ramzuiv/sandbox/Cubic Formula
  • eo.wikipedia.org üzerinde kullanımı
    • Kuba ekvacio
  • es.wikipedia.org üzerinde kullanımı
    • Ecuación de tercer grado
    • Anexo:Curvas
  • eu.wikipedia.org üzerinde kullanımı
    • Aljebra
    • Funtzio kubiko

Bu dosyanın daha fazla küresel kullanımını görüntüle.

Üstveri

Bu dosyada, muhtemelen fotoğraf makinesi ya da tarayıcı tarafından eklenmiş ek bilgiler mevcuttur. Eğer dosyada sonradan değişiklik yapıldıysa, bazı bilgiler yeni değişikliğe göre eski kalmış olabilir.

Kısa başlıkPolynomial of degree 3
Resim başlığıy=\frac{1}{4}x^3+\frac{3}{4}x^2-\frac{3}{2}x-2
Genişlik400
Yükseklik400
"https://tr.wikipedia.org/wiki/Dosya:Polynomialdeg3.svg" sayfasından alınmıştır
  • Gizlilik politikası
  • Vikipedi hakkında
  • Sorumluluk reddi
  • Davranış Kuralları
  • Geliştiriciler
  • İstatistikler
  • Çerez politikası
  • Mobil görünüm
  • Wikimedia Foundation
  • Powered by MediaWiki
Dosya:Polynomialdeg3.svg
Konu ekle