İntegral Testi Matematikte integral testi veya bir diğer deyişle yakınsaklık için integral testi , terimleri negatif olmayan sonsuz serilerin yakınsaklığını belirlemek için kullanılan bir yöntemdir. Bu testin erken bir versiyonu 14. yüzyılda Hint matematikçi Madhava ve takipçileri tarafından bulunmuştur. Avrupa'da ise Maclaurin ve Cauchy tarafından geliştirilmiş olup aynı zamanda Maclaurin-Cauchy testi olarak da bilinir.
Bir N tam sayısını ve sınırsız [N , ∞) aralığında tanımlı monoton azalan bir f fonksiyonunu ele alalım. O zaman,
∑
n
=
N
∞
f
(
n
)
{\displaystyle \sum _{n=N}^{\infty }f(n)}
serisi ancak ve ancak
∫
N
∞
f
(
x
)
d
x
{\displaystyle \int _{N}^{\infty }f(x)\,dx}
integrali sonlu ise, yakınsaktır. Özelde, integral ıraksar ise, o zaman seri de ıraksar.
İspat basit bir şekilde f (n ) terimini f 'nin [n − 1, n ] ve [n , n + 1] aralıkları üzerindeki integralleriyle karşılaştırarak, karşılaştırma testini kullanmaktadır
f , monoton azalan bir fonksiyon olduğu için,
f
(
x
)
≤
f
(
n
)
,
x
∈
[
n
,
∞
)
{\displaystyle f(x)\leq f(n)\quad {\text{, }}x\in [n,\infty )}
ve
f
(
n
)
≤
f
(
x
)
,
x
∈
[
N
,
n
]
,
{\displaystyle f(n)\leq f(x)\quad {\text{, }}x\in [N,n],}
olduğunu biliyoruz. Bu yüzden, N 'den büyük n için,
∫
n
n
+
1
f
(
x
)
d
x
≤
∫
n
n
+
1
f
(
n
)
d
x
=
f
(
n
)
=
∫
n
−
1
n
f
(
n
)
d
x
≤
∫
n
−
1
n
f
(
x
)
d
x
.
{\displaystyle \int _{n}^{n+1}f(x)\,dx\leq \int _{n}^{n+1}f(n)\,dx=f(n)=\int _{n-1}^{n}f(n)\,dx\leq \int _{n-1}^{n}f(x)\,dx.}
Alt tahmin de aynı zamanda f (N ) için geçerli olduğu için, N 'den belli bir M (M , N 'den büyüktür) tam sayısına kadar n üzerinden toplamlarla
∫
N
M
+
1
f
(
x
)
d
x
≤
∑
n
=
N
M
f
(
n
)
≤
f
(
N
)
+
∫
N
M
f
(
x
)
d
x
{\displaystyle \int _{N}^{M+1}f(x)\,dx\leq \sum _{n=N}^{M}f(n)\leq f(N)+\int _{N}^{M}f(x)\,dx}
elde ederiz. M sonsuza giderse, sonucu elde ederiz.
Harmonik seri
∑
n
=
1
∞
1
n
{\displaystyle \sum _{n=1}^{\infty }{\frac {1}{n}}}
ıraksar çünkü doğal logaritmayı , türevini ve hesabın temel teoremini kullanarak
∫
1
M
1
x
d
x
=
ln
x
|
1
M
=
ln
M
→
∞
,
M
→
∞
iken
.
{\displaystyle \int _{1}^{M}{\frac {1}{x}}\,dx=\ln x{\Bigr |}_{1}^{M}=\ln M\to \infty {\text{,}}\quad M\to \infty \quad {\text{iken}}.}
elde edilir.
Tersine,
∑
n
=
1
∞
1
n
1
+
ε
{\displaystyle \sum _{n=1}^{\infty }{\frac {1}{n^{1+\varepsilon }}}}
serisi (Riemann zeta fonksiyonu ile karşılaştırınız) her ε > 0 için yakınsar çünkü
∫
1
M
1
x
1
+
ε
d
x
=
−
1
ε
x
ε
|
1
M
=
1
ε
(
1
−
1
M
ε
)
≤
1
ε
,
∀
M
≥
1.
{\displaystyle \int _{1}^{M}{\frac {1}{x^{1+\varepsilon }}}\,dx=-{\frac {1}{\varepsilon x^{\varepsilon }}}{\biggr |}_{1}^{M}={\frac {1}{\varepsilon }}{\Bigl (}1-{\frac {1}{M^{\varepsilon }}}{\Bigr )}\leq {\frac {1}{\varepsilon }}{\text{,}}\quad \forall M\geq 1.}
Yukarıdaki harmonik serileri de içeren örnekler şu soruyu beraberinde getirir: Terimleri f (n ) olan ve 1/n 'den daha hızlı bir şekilde 0'a doğru azalan; ancak, 1/n 1+ε 'dan her ε > 0 için
lim
n
→
∞
f
(
n
)
1
/
n
=
0
ve
lim
n
→
∞
f
(
n
)
1
/
n
1
+
ε
=
∞
{\displaystyle \lim _{n\to \infty }{\frac {f(n)}{1/n}}=0\quad {\text{ve}}\quad \lim _{n\to \infty }{\frac {f(n)}{1/n^{1+\varepsilon }}}=\infty }
bağlamında 0'a doğru daha yavaş azalan monoton bir seri var mı ve bu seri yine de ıraksar mı? Böyle bir seri bulunur bulunmaz, aynı soru 1/n 'nin yerini almış f (n ) ile de sorulabilir vs. Bu yolla, ıraksaklık ve yakınsaklık arasındaki sınır çizgisini araştırmak mümkündür.
İntegral testini kullanarak, her k doğal sayısı için
∑
n
=
N
k
∞
1
n
ln
(
n
)
ln
2
(
n
)
⋯
ln
k
−
1
(
n
)
ln
k
(
n
)
{\displaystyle \sum _{n=N_{k}}^{\infty }{\frac {1}{n\ln(n)\ln _{2}(n)\cdots \ln _{k-1}(n)\ln _{k}(n)}}}
serisinin hala ıraksadığı gösterilebilir (k = 1 için, asalların terslerinin toplamı ıraksar ile karşılaştırınız.); ancak
∑
n
=
N
k
∞
1
n
ln
(
n
)
ln
2
(
n
)
⋯
ln
k
−
1
(
n
)
(
ln
k
(
n
)
)
1
+
ε
{\displaystyle \sum _{n=N_{k}}^{\infty }{\frac {1}{n\ln(n)\ln _{2}(n)\cdots \ln _{k-1}(n)(\ln _{k}(n))^{1+\varepsilon }}}}
serisi her ε > 0 için yakınsar. Burada, lnk k kere bileşkesinin alınmasını göstermektedir:
ln
k
(
x
)
=
{
ln
(
x
)
,
k
=
1
,
ln
(
ln
k
−
1
(
x
)
)
,
k
≥
2.
{\displaystyle \ln _{k}(x)={\begin{cases}\ln(x)&{\text{, }}k=1,\\\ln(\ln _{k-1}(x))&{\text{, }}k\geq 2.\end{cases}}}
Dahası, N k k bileşkenin iyi tanımlı olduğu ve lnk N k
N
k
≥
e
e
⋅
⋅
e
⏟
k
tane
e
=
e
↑↑
k
.
{\displaystyle N_{k}\geq \underbrace {e^{e^{\cdot ^{\cdot ^{e}}}}} _{k\ {\text{tane}}\ e}=e\uparrow \uparrow k.}
İlk serinin ıraksaklığını integral testi ile görmek için, zincir kuralının arka arkaya kullanımının
d
d
x
ln
k
+
1
(
x
)
=
d
d
x
ln
(
ln
k
(
x
)
)
=
1
ln
k
(
x
)
d
d
x
ln
k
(
x
)
=
⋯
=
1
x
ln
(
x
)
⋯
ln
k
(
x
)
,
{\displaystyle {\frac {d}{dx}}\ln _{k+1}(x)={\frac {d}{dx}}\ln(\ln _{k}(x))={\frac {1}{\ln _{k}(x)}}{\frac {d}{dx}}\ln _{k}(x)=\cdots ={\frac {1}{x\ln(x)\cdots \ln _{k}(x)}},}
verdiğini görmemiz gerekir. Bu yüzden
∫
N
k
∞
d
x
x
ln
(
x
)
⋯
ln
k
(
x
)
=
ln
k
+
1
(
x
)
|
N
k
∞
=
∞
.
{\displaystyle \int _{N_{k}}^{\infty }{\frac {dx}{x\ln(x)\cdots \ln _{k}(x)}}=\ln _{k+1}(x){\bigr |}_{N_{k}}^{\infty }=\infty .}
İkinci serinin yakınsaklığını görmek için, kuvvet serisi , zincir kuralı ve yukarıdaki sonucun
−
d
d
x
1
ε
(
ln
k
(
x
)
)
ε
=
1
(
ln
k
(
x
)
)
1
+
ε
d
d
x
ln
k
(
x
)
=
⋯
=
1
x
ln
(
x
)
⋯
ln
k
−
1
(
x
)
(
ln
k
(
x
)
)
1
+
ε
{\displaystyle -{\frac {d}{dx}}{\frac {1}{\varepsilon (\ln _{k}(x))^{\varepsilon }}}={\frac {1}{(\ln _{k}(x))^{1+\varepsilon }}}{\frac {d}{dx}}\ln _{k}(x)=\cdots ={\frac {1}{x\ln(x)\cdots \ln _{k-1}(x)(\ln _{k}(x))^{1+\varepsilon }}}}
verdiğini görmeliyiz. Bu yüzden,
∫
N
k
∞
d
x
x
ln
(
x
)
⋯
ln
k
−
1
(
x
)
(
ln
k
(
x
)
)
1
+
ε
=
−
1
ε
(
ln
k
(
x
)
)
ε
|
N
k
∞
<
∞
{\displaystyle \int _{N_{k}}^{\infty }{\frac {dx}{x\ln(x)\cdots \ln _{k-1}(x)(\ln _{k}(x))^{1+\varepsilon }}}=-{\frac {1}{\varepsilon (\ln _{k}(x))^{\varepsilon }}}{\biggr |}_{N_{k}}^{\infty }<\infty }
olur.
Knopp, Konrad, "Infinite Sequences and Series", Dover publications, Inc., New York, 1956. (&; 3.3) ISBN 0-486-60153-6
Whittaker, E. T., and Watson, G. N., A Course in Modern Analysis , 4. baskı, Cambridge University Press, 1963. (§ 4.43) ISBN 0-521-58807-3 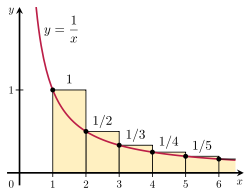




![{\displaystyle f(n)\leq f(x)\quad {\text{, }}x\in [N,n],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b40086403d03aa39c6ee41c53383e8cecc8806da)














