Simit (geometri)

Simit

Topolojide ve geometride simit (torus) bir yüzeydir. Üç boyutlu uzayda bir çemberin, aynı düzlemde yatan ve çembere değmeyen bir doğru etrafında döndürülmesiyle elde edilir. Yiyecek simidin ya da yüzmek için kullanılan şişirilmiş iç lastiğin yüzeyi matematiksel olarak birer simittir.

Simit topolojik olarak bir çemberle (S¹) kendisinin çarpımı (S¹ × S¹) olarak tanımlanır. (İki boyutlu) Simit genelde T² olarak gösterilir. Bu çarpım aracılığıyla üzerinde çarpım topolojisi kurulmuştur. Bir yüzey olarak kapalıdır (tıkız ve kenarsız).

Böyle tanımlanmış topolojik simit doğal olarak karmaşık 2 boyutlu (gerçel 4 boyutlu) karmaşık vektör uzayı C²'de bulunabilir. C 'de S¹ birim çemberini düşünelim. C²'nin her bir C kopyasında bulunan birim çemberlerin çarpımı C²'de bir simit tanımlayacaktır. Bu simide Clifford simidi denir. Bu simidin her noktası C²'de başnoktadan (orijin) ${\sqrt {2}}$ kadar uzaktadır. Dolayısıyla Clifford simidi C²'de üç boyutlu küre (S³) içinde yatar.

Bir simidi topolojik olarak tanımlamanın birçok yolu vardır. Örneğin düzlemde K=[0,1] × [0,1] birim karesi üzerinde şöyle bir denklik bağıntısı tanımlayalım. Her nokta kendisine; sol kenardaki her bir nokta, sağ kenarda karşısındaki noktaya; alt kenardaki her bir nokta, üst kenarda karşısındaki noktaya denk olsun:

(x,y) ~ (x,y); (0,y) ~ (1,y); (x,0) ~ (x,1).

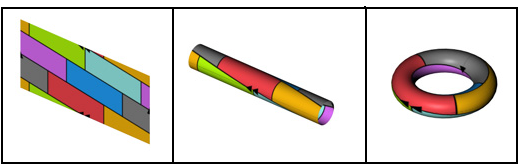
K topolojik uzayı bu denklik bağıntısına bölündüğünde ortaya çıkan bölüm uzayı yukarıda tarif edilen simide homeomorfiktir; yani topolojik olarak eştirler. Bu işlem aslında şöyle hayal edilebilir: kare bir kağıdın önce alt ve üst kenarları, sonra sol ve sağ kenarları yapıştırılıyor. Elde edilen yüzey bir simittir.

Yukarıdaki inşaya benzer bir biçimde, a ve b sıfırdan farklı iki gerçel sayı olmak üzere, R² düzlemi, üzerinde tanımlanan

(x,y) ~ (x+a,y) ~ (x,y+b)

denklik bağıntısına bölündüğünde çıkan bölüm uzayı da simide homeomorfiktir.

Dış bağlantılar

• Creation of a torus19 Nisan 2006 tarihinde Wayback Machine sitesinde arşivlendi.
• "4D torus" 14 Nisan 2012 tarihinde Wayback Machine sitesinde arşivlendi.
• "Relational Perspective Map" 28 Şubat 2021 tarihinde Wayback Machine sitesinde arşivlendi.
• "Torus Games" 2 Haziran 2012 tarihinde Wayback Machine sitesinde arşivlendi.
• Polydos