Çarpanlara ayırma

x² + cx + d = (x + a)(x + b)

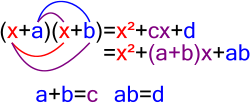
Çarpanlara ayırma, bir polinomun, tam sayının ya da matrisin kendisini oluşturan bileşenlerin çarpımı şeklinde yazılmasıdır. Örneğin 15 sayısı 3 ve 5 asal sayılarının çarpımı şeklinde yazılabilir: 3 × 5 ya da x² − 4 polinomu (x − 2)(x + 2) şeklinde yazılabilir.

Çarpanlara ayırmadaki temel amaç bir bütünü daha küçük yapılara ayırmaktır; sayıları asal sayıların çarpımı, polinomları indirgenemeyen polinomların çarpımı şeklinde yazmak gibi. Çarpanlara ayırmanın tersi genişletmedir.

Asal çarpanlarına ayırma çok büyük sayılar için zor bir problemdir. Bu problemin bilinen bir çözümü yoktur. Bu yüzden RSA gibi açık anahtarlı şifreleme yöntemlerinde kullanılır.

Tam sayılar

Ana madde: Asal çarpanlara ayırma

Aritmetiğin temel teoremine göre 1'den büyük her tam sayı asal sayıların çarpımı şeklinde yazılabilir.

Bir n tam sayısını çarpanlara ayırmak için, n'nin bölenini q'yu bulmak veya n'nin asal olduğuna karar vermek için bir algoritmaya gerek vardır. Böyle bir bölen bulunduğunda, bu algoritmanın q ve n / q çarpanlarına tekrar tekrar uygulanması, sonunda n'nin tam çarpanlara ayrılmasını sağlar.

n'nin bir q bölenini bulmak için, 1 < q ve q² ≤ n olacak şekilde q'nun tüm değerlerini test etmek yeterlidir. Aslında, eğer r, r² > n olacak şekilde n'nin bir böleniyse, o zaman q² ≤ n olacak şekilde q = n / r, n'nin bir bölenidir.

q'nun değerleri artan sırada denenirse, bulunan ilk bölen mutlaka bir asal sayıdır ve r = n / q ortak çarpanının q'dan küçük herhangi bir böleni olamaz. Tam çarpanları bulmak için, r'nin q'dan küçük ve √r'den büyük olmayan bir bölenini arayarak algoritmaya devam etmek yeterlidir.

Yöntemi uygulamak için q'nun tüm değerlerini denemeye gerek yoktur. Prensip olarak, sadece asal bölenleri denemek yeterlidir. Bunun, örneğin Eratosten kalburu ile üretilebilecek bir asal sayılar tablosuna sahip olması gerekir. Çarpanlara ayırma yöntemi esas olarak Eratosthenes'in eleği ile aynı işi yaptığından, yalnızca asal olup olmadıkları hemen belli olmayan sayıları bölen için denemek genellikle daha kolaydır. Tipik olarak, 2, 3, 5 ve son hanesi 1, 3, 7, 9 olan ve rakamların toplamı 3'ün katı olmayan > 5 sayıları test edilerek ilerlenebilir.

Bu yöntem, küçük tam sayıları çarpanlara ayırmak için iyi çalışır, ancak daha büyük tam sayılar için verimsizdir. Örneğin, Pierre de Fermat, 6. Fermat sayısının

$1+2^{2^{5}}=1+2^{32}=4\,294\,967\,297$

'nin asal sayı olmadığını keşfedemedi. Aslında yukarıdaki yöntemi uygulamak, 10  ondalık basamaklı bir sayı için 10.000'den fazla bölme gerektirir.

Daha verimli çarpanlara ayırma algoritmaları vardır. Ancak nispeten verimsiz kalırlar, çünkü tekniğin mevcut durumu ile, rastgele seçilen iki asal sayının çarpımı olan 500 ondalık basamaklı bir sayı daha güçlü bilgisayarlarla bile çarpanlara ayrılamaz. Bu, güvenli internet iletişimi için yaygın kullanılan RSA şifreleme sisteminin güvenliğini sağlar.

Örnek

n = 1386'yı asal sayılara ayırmak için:

• 2:'ye bölme ile başlayın: sayı çifttir ve n = 2 · 693. Birinci bölen adayı olarak 693 ve 2 ile devam edin.
• 693 tektir (2 bölen değildir), ancak 3:'ün katıdır: biri 693 = 3 · 231 ve n = 2 · 3 · 231'e sahiptir. 231 ve birinci bölen adayı olarak 3 ile devam edin.
• 231 aynı zamanda 3:'ün katıdır: 231 = 3 · 77 ve dolayısıyla n = 2 · 3² · 77 vardır. Birinci bölen adayı olarak 77 ve 3 ile devam edin.
• 77, 3'ün katı değildir, çünkü rakamlarının toplamı 14'tür, 3'ün katı değildir. Son basamağı 7 olduğu için 5'in katı da değildir. Test edilecek bir sonraki tek bölen 7'dir. 77 = 7 · 11 ve dolayısıyla n = 2 · 3² · 7 · 11. Bu, 7'nin asal olduğunu gösterir (doğrudan test edilmesi kolaydır). Birinci bölen adayı olarak 11 ve 7 ile devam edin.
• 7² > 11 olarak biri bitti. Böylece 11 asaldır ve asal çarpanlara ayırma

1386 = 2 · 3² · 7 · 11.

Polinomlar

Karesel polinomlar

$ax^{2}+bx+c$ şeklindeki her karesel polinom,

$a(x-{\frac {-b+{\sqrt {b^{2}-4ac}}}{2a}})(x-{\frac {-b-{\sqrt {b^{2}-4ac}}}{2a}})$ şeklinde çarpanlarına ayrılabilir.

Karesel özdeşlikler

(a + b)² = a² + 2ab + b²

Aşağıdaki özdeşlikler kullanılarak bazı polinomlar kolayca çarpanlarına ayrılabilir.

$a^{2}+2ab+b^{2}=(a+b)^{2},\,\!$

ve

$a^{2}-2ab+b^{2}=(a-b)^{2}.\,\!$

Örneğin,

$x^{2}+6x+9=(x+3)^{2}$

İki kare toplamı/farkı

İki kare farkı,

$a^{2}-b^{2}=(a+b)(a-b),\,\!$

Eğer iki kare toplam halindeyse karmaşık sayı cinsinden çarpanlarına ayrılır,

$a^{2}+b^{2}=(a+bi)(a-bi).\,\!$

Gruplandırarak çarpanlara ayırma

Birden çok değişkenin olduğu bir ifadede önce benzer terimler bir araya getirilip ortak çarpan parantezine alınır, ardından oluşan diğer ortak terim de paranteze alınır. Örneğin,

$4x^{2}+20x+3yx+15y\,$

Benzer terimler bir araya getirlir, $(4x^{2}+20x)+(3yx+15y)\,$

Ortak çarpan parantezine alınır,$4x(x+5)+3y(x+5)\,$

Oluşan yeni ortak terim de paranteze alınır $(x+5)(4x+3y)\,$

Dış bağlantılar

• Wolfram Alpha, polinomları ve sayıları çarpanalarına ayırır.28 Mart 2019 tarihinde Wayback Machine sitesinde arşivlendi.