Dosya:Stationary vs inflection pts.svg - Vikipedi
İçeriğe atla
Ana menü
Gezinti
  • Anasayfa
  • Hakkımızda
  • İçindekiler
  • Rastgele madde
  • Seçkin içerik
  • Yakınımdakiler
Katılım
  • Deneme tahtası
  • Köy çeşmesi
  • Son değişiklikler
  • Dosya yükle
  • Topluluk portalı
  • Wikimedia dükkânı
  • Yardım
  • Özel sayfalar
Vikipedi Özgür Ansiklopedi
Ara
  • Bağış yapın
  • Hesap oluştur
  • Oturum aç
  • Bağış yapın
  • Hesap oluştur
  • Oturum aç

Dosya:Stationary vs inflection pts.svg

Sayfa içeriği diğer dillerde desteklenmemektedir.
  • Dosya
  • Tartışma
  • Oku
  • Wikimedia Commons üzerinde gör
  • Yerel açıklama ekle
  • Yerel açıklama kaynağı ekle
Araçlar
Eylemler
  • Oku
  • Wikimedia Commons üzerinde gör
  • Yerel açıklama ekle
  • Yerel açıklama kaynağı ekle
Genel
  • Sayfaya bağlantılar
  • Basılmaya uygun görünüm
  • Sayfa bilgisi
  • Kısaltılmış URL'yi al
  • Karekodu indir
Diğer projelerde
Görünüm
Vikipedi, özgür ansiklopedi
  • Dosya
  • Dosya geçmişi
  • Dosya kullanımı
  • Küresel dosya kullanımı
Dosya:Stationary vs inflection pts.svg
Bu SVG dosyasının PNG önizlemesinin boyutu: 479 × 297 piksel. Diğer çözünürlükler: 320 × 198 piksel | 640 × 397 piksel | 1.024 × 635 piksel | 1.280 × 794 piksel | 2.560 × 1.587 piksel.
Tam çözünürlük (SVG dosyası, sözde 479 × 297 piksel, dosya boyutu: 32 KB)
Bu dosya Wikimedia Commons'ta bulunmaktadır. Dosyanın açıklaması aşağıda gösterilmiştir.
Commons, serbest/özgür telifli medya dosyalarının bulundurulduğu depodur. Siz de yardım edebilirsiniz.
Bu dosya Wikimedia Commons'ta bulunmaktadır.

Özet

AçıklamaStationary vs inflection pts.svg
English: Graph of f ( x ) = x + sin ⁡ ( 2 x ) {\displaystyle f(x)=x+\sin(2x)} {\displaystyle f(x)=x+\sin(2x)} and shows stationary points (red circles) and inflection points (blue squares). The stationary points in this graph are all relative maxima or relative minima.
Tarih 19 Ekim 2011
Kaynak

Mathematica source code: 

f := #1 + Sin[2 #1] &;
inflectionPoints = Table[{x, f[x]}, {x, -Pi, Pi, Pi/2}];
stationaryPoints = Union[Table[{x, f[x]}, {x, -2 Pi/3, Pi/3, Pi}], Table[{x, f[x]}, {x, -Pi/3, 2 Pi/3, Pi}]];
Show[Plot[f[x], {x, -Pi - 1, Pi + 1}], ListPlot[{stationaryPoints, inflectionPoints}, PlotMarkers -> {{Graphics@{Red, Disk[]}, 0.05}, {Graphics@{Blue, Rectangle[]}, 0.05}}], ImageSize -> 500]

After saving the image as an SVG from Mathematica, edit the raw SVG text by adding "width='479' height='297'" to the end of the SVG tag.
Yazar Self (with some Mathematica help)
SVG gelişimi
InfoField
 Bu SVG kaynak kodu geçerlidir.
 Bu vektörel grafik Mathematica ile oluşturuldu.
 Bu SVG dosyası, gömülü metin/dijitaler kullanır.

Lisanslama

Ben, bu işin telif sahibi, burada işi aşağıdaki lisanslar altında yayımlıyorum:
GNU head Bu belgenin GNU Özgür Belgeleme Lisansı, Sürüm 1.2 veya Özgür Yazılım Vakfı tarafından yayımlanan sonraki herhangi bir sürüm şartları altında bu belgenin kopyalanması, dağıtılması ve/veya değiştirilmesi için izin verilmiştir;

Değişmeyen Bölümler, Ön Kapak Metinleri ve Arka Kapak Metinleri yoktur. Lisansın bir kopyası GNU Özgür Belgeleme Lisansı sayfasında yer almaktadır.http://www.gnu.org/copyleft/fdl.htmlGFDLGNU Free Documentation Licensetruetrue

w:tr:Creative Commons
atıf benzer paylaşım
Bu dosya, Creative Commons Atıf-Benzer Paylaşım 3.0 Taşınmamış lisansı ile lisanslanmıştır
Şu seçeneklerde özgürsünüz:
  • paylaşım – eser paylaşımı, dağıtımı ve iletimi
  • içeriği değiştirip uyarlama – eser adaptasyonu
Aşağıdaki koşullar geçerli olacaktır:
  • atıf – Esere yazar veya lisans sahibi tarafından belirtilen (ancak sizi ya da eseri kullanımınızı desteklediklerini ileri sürmeyecek bir) şekilde atıfta bulunmalısınız.
  • benzer paylaşım – Maddeyi yeniden düzenler, dönüştürür veya inşa ederseniz, katkılarınızı özgünüyle aynı veya uyumlu lisans altında dağıtmanız gerekir.
https://creativecommons.org/licenses/by-sa/3.0CC BY-SA 3.0 Creative Commons Attribution-Share Alike 3.0 truetrue
İstediğiniz lisansı seçebilirsiniz.

Altyazılar

Bu dosyanın temsil ettiği şeyin tek satırlık açıklamasını ekleyin.
Graph of f(x) = x + sin(2x), which shows stationary points as red circles, and inflection points as blue squares. The stationary points are all relative minima or maxima.
Courbe représentative de la fonction f(x) = x + sin(2x) montrant les points stationnaires par des cercles rouges, et les points d'inflexion par des carrés bleus. Les points stationnaires sont des minimums et maximums locaux.

Bu dosyada gösterilen öğeler

betimlenen

telif hakkı durumu

telif hakkı alınmış

telif hakkı lisansı

GNU Free Documentation License, version 1.2 or later İngilizce

Creative Commons Atıf-AynıLisanslaPaylaş 3.0 Yerelleştirilmemiş

kuruluşu

19 Ekim 2011

Dosya geçmişi

Dosyanın herhangi bir zamandaki hâli için ilgili tarih/saat kısmına tıklayın.

Tarih/SaatKüçük resimBoyutlarKullanıcıYorum
güncel15.48, 19 Ekim 201115.48, 19 Ekim 2011 tarihindeki sürümün küçültülmüş hâli479 × 297 (32 KB)Bender2k14Added default image dimensions
15.37, 19 Ekim 2011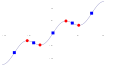15.37, 19 Ekim 2011 tarihindeki sürümün küçültülmüş hâli512 × 512 (32 KB)Bender2k14Smaller nominal dimensions
15.30, 19 Ekim 201115.30, 19 Ekim 2011 tarihindeki sürümün küçültülmüş hâli512 × 512 (32 KB)Bender2k14{{Information |Description ={{en|1=Graph shows stationary points (red circles) and inflection points (blue squares). The stationary points in this graph are all relative maxima or relative minima.}} |Source =Mathematica sour

Dosya kullanımı

Bu görüntü dosyasına bağlantısı olan sayfalar:

  • Durgunluk noktası

Küresel dosya kullanımı

Aşağıdaki diğer vikiler bu dosyayı kullanmaktadır:

  • ar.wikipedia.org üzerinde kullanımı
    • نقطة حرجة (رياضيات)
    • نقطة مستقرة
  • ckb.wikipedia.org üzerinde kullanımı
    • خاڵی قەیرانی (ماتماتیک)
  • cs.wikipedia.org üzerinde kullanımı
    • Funkce (matematika)
    • Stacionární bod
  • cv.wikipedia.org üzerinde kullanımı
    • Кризисла пăнчă (математика)
  • en.wikipedia.org üzerinde kullanımı
    • Stationary point
    • Critical point (mathematics)
    • User:Bender2k14/My Images
  • fa.wikipedia.org üzerinde kullanımı
    • نقطه بحرانی (ریاضیات)
  • fr.wikipedia.org üzerinde kullanımı
    • Point stationnaire
  • he.wikipedia.org üzerinde kullanımı
    • טיוטה:נקודות קריטיות
  • id.wikipedia.org üzerinde kullanımı
    • Titik stasioner
    • Titik kritis (matematika)
  • it.wikipedia.org üzerinde kullanımı
    • Punto critico (matematica)
  • ja.wikipedia.org üzerinde kullanımı
    • 臨界点 (数学)
  • ro.wikipedia.org üzerinde kullanımı
    • Punct staționar
  • sl.wikipedia.org üzerinde kullanımı
    • Stacionarna točka
  • ta.wikipedia.org üzerinde kullanımı
    • மாறுநிலை எண் (கணிதம்)
  • vi.wikipedia.org üzerinde kullanımı
    • Điểm cực trị
    • Giếng thế năng
    • Điểm dừng (toán học)
  • zh.wikipedia.org üzerinde kullanımı
    • 驻点
    • 临界点 (数学)
"https://tr.wikipedia.org/wiki/Dosya:Stationary_vs_inflection_pts.svg" sayfasından alınmıştır
  • Gizlilik politikası
  • Vikipedi hakkında
  • Sorumluluk reddi
  • Davranış Kuralları
  • Geliştiriciler
  • İstatistikler
  • Çerez politikası
  • Mobil görünüm
  • Wikimedia Foundation
  • Powered by MediaWiki
Dosya:Stationary vs inflection pts.svg
Konu ekle