Logaritma

İkilik logaritmanın grafiği. Eğri (2,1), (4,2) ve (8,3) noktalarından geçer. y ekseniyle hiçbir zaman kesişmez.)

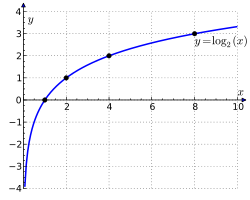
Matematikte logaritma, üstel fonksiyonların tersi olan bir matematiksel fonksiyondur. Mesela, 1000'in 10 tabanına göre logaritması 3'tür çünkü 1000, 10'un 3. kuvvetidir, 1000 = 10 × 10 × 10 = 10³. Daha genel bir ifadeyle:

$x=b^{y}\Leftrightarrow log_{b}(x)=y$

Tabanın 10 olması durumunda işlev, onluk logaritma ya da genel logaritma olarak adlandırılır. Onluk logaritmanın fen ve mühendislikte pek çok kullanım alanı vardır. Taban e sayısı olursa buna doğal logaritma denir. Doğal logaritma, soyut matematikte çok sık kullanılır. Bir diğer logaritma şekli de ikilik logaritmadır, bilgisayar bilimlerinde önemli bir yere sahiptir.

Logaritma 17. yüzyılın başında John Napier tarafından hesaplamaları kolaylaştırmak için oluşturuldu. Denizciler, bilim insanları, mühendisler ve daha hızlı hesap yapmak isteyen kişiler tarafından hızlıca benimsenen logaritma, hesap cetvelleri ve logaritma tabloları aracılığıyla kullanılabiliyordu. Uzun zaman alan çok basamaklı çarpma işlemleri logaritmanın şu özelliği sayesinde oldukça kolaylaştı:

$\log _{b}(xy)=\log _{b}(x)+\log _{b}(y).\,$

Logaritmanın bugünkü yazım şekli 18. yüzyıla dayanır. Leonhard Euler logaritmanın üstel işlevlerle olan ilişkisini keşfetmiş ve bugünkü yazımı oluşturmuştur.

Gerekliliği ve tanımı

Logaritma, üstel işlevlerin tersinin hesaplanmasına duyulan ihtiyaç sonucu ortaya çıkmıştır. Örneğin 2'nin küpü 8'dir. Burada 3'ü ifade etmek için logaritmaya ihtiyaç vardır. log₂ 8 = 3.

Tarihi

Logaritma, birbirinden habersiz çalışan iki kişi tarafından keşfedilmiştir. Bunlar; 1614'te İskoçyalı John Napier ve 1620'de İsviçreli Joost Bürgi'dir.

Logaritmaya önemli katkı sağlayan bir diğer isim de cebirin babası olarak tanınan Fars matematikçi Harezmi'dir. Aynı zamanda ondalık sayıyı bulmuştur ve sıfırı kullanan ilk kişidir. 780-850 yılları arasında yaşamıştır.

Logaritma üzerinde önemli çalışmaları olan bir Türk matematikçi Gelenbevi İsmail Efendi'dir. Kendisi büyük bir matematikçi olup, mantıkla da uğraşmıştır. 1730-1790 yıllarında yaşayan bu büyük alimin Logaritma Risalesi isimli çok açık, anlaşılır yazılmış bir eseri mevcuttur. Bu risaledeki metinler, bilim insanlarına hesap yapabilen bir cihaz tasarlama fikrini vermiştir. İsmail Efendi'nin bilim dünyasına bu açıdan bakıldığında büyük katkıları olduğu açıkça fark edilmektedir. Logaritmanın Türkiye'ye gelişine ve uygulanışına dair en detaylı bilgileri veren bilimsel bir makalede bu konu bilim tarihi bakımından ve Salih Murat Üzdilek'in hatıralarıyla beraber açıklanmakta ve Türkiye'de logaritma konusunda ilk çalışmanın Halifezade İsmail Efendi tarafından 1765 yılında yayınlanan Tuhfe-i Behic-i Rasini Tercüme-i Zic-i Kasini adlı yazma tercüme eser olduğu ve logaritmanın Türkiye'ye Batı'dan J. Cassini üzerinden yapılma tercümeyle geldiğini kabul etmek gerektiği gösterilmektedir.

Logaritmik özellikler

Logaritma: log₁₀ (sarı),
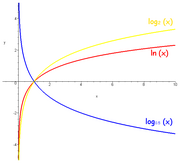
ln (kırmızı) ve log_½ (mavi)

Çarpma, bölme, üs ve kök

	Özellik	Örnek
çarpma	$\log _{b}(xy)=\log _{b}(x)+\log _{b}(y)\,$	$\log _{3}(243)=\log _{3}(9\cdot 27)=\log _{3}(9)+\log _{3}(27)=2+3=5\,$
bölme	$\log _{b}\!\left({\frac {x}{y}}\right)=\log _{b}(x)-\log _{b}(y)\,$	$\log _{2}(16)=\log _{2}\!\left({\frac {64}{4}}\right)=\log _{2}(64)-\log _{2}(4)=6-2=4$
üs	$\log _{b}(x^{p})=p\log _{b}(x)\,$	$\log _{2}(64)=\log _{2}(2^{6})=6\log _{2}(2)=6\,$
kök	$\log _{b}{\sqrt[{p}]{x}}={\frac {\log _{b}(x)}{p}}\,$	$\log _{10}{\sqrt {1000}}={\frac {1}{2}}\log _{10}1000={\frac {3}{2}}=1.5$

Taban değiştirme

$\log _{b}(x)={\frac {\log _{k}(x)}{\log _{k}(b)}}.\,$

Hesap makineleri istenen logaritma değerini hesaplamak için şu formülü kullanır:

$\log _{b}(x)={\frac {\log _{10}(x)}{\log _{10}(b)}}={\frac {\log _{e}(x)}{\log _{e}(b)}}.\,$

Özel tabanlar

Yaygın olarak kullanılan üç tane taban vardır.

Taban	İsim logb(x)	ISO gösterimi	Diğer gösterimler	Kullanıldığı alanlar
e	doğal logaritma	ln(x)		matematiksel inceleme, fizik, kimya, istatistik, ekonomi
2	ikili logaritma	lb(x)	ld(x), log(x), lg(x), log2(x)	bilgisayar bilimi, bilgi kuramı, matematik, müzik kuramı
10	adi logaritma	lg(x)	"log(x)" (mühendislik, biyoloji, astronomi), log10(x)	çeşitli mühendislik alanları (bkz. desibel), logaritma tabloları, hesap makinesi, spektroskopi

$\ln {x}=\log _{2.718281828459045\ldots }{x}=\int _{1}^{x}1/t{\text{dt}}\approx 0.01\log _{1.01005}{x}\approx \log _{4}{x}+\log _{36}{x}$

Negatif ve imajiner logaritma

Negatif logaritma üzerinde en önemli çalışmalar yapan matematikçi Leonhard Euler dir.

Euler özdeşliği yardımıya negatif sayıların logaritması alınabilir. Bu logaritmayı alabilmek için logaritmanın özellikleri ve Euler özdeşliği bilinmelidir.

$e^{i\pi }+1=0$ İşte negatif ve imajiner logaritmanın en önemli denklemlerinden biridir. Euler özdeşliği.

$a^{x}=-b$ denkleminin çözümü $x=log_{a}(-b)\Rightarrow x=log_{a}b+log_{a}(-1)$ olur.

Burada $log_{a}(-1)={\frac {ln(-1)}{lna}}$ şeklinde de yazılabilir. Bu logaritmanın ln ile genişletmesinin sebebi $e^{i\pi }+1=0$ denklemi uygun bir logaritma olan ln logaritma fonksiyonudur.

$e^{i\pi }+1=0\Rightarrow e^{i\pi }=-1\Rightarrow i\pi =ln(-1)$ olur. $log_{a}(-1)={\frac {ln(-1)}{lna}}$ denkleminde yerine yazılırsa $log_{a}(-1)={\frac {i\pi }{lna}}$ olur. Bu sonuç da $x=log_{a}b+log_{a}(-1)$ denkleminde yerine yazılırsa

$x=log_{a}b+{\frac {i\pi }{lna}}$ sonucuna ulaşılır.

Sonuç

$a^{x}=-b\Rightarrow x=log_{a}b+{\frac {i\pi }{lna}}$

İmajiner logaritma

Sanal logaritma demektir. Sanal sayılar ı içerir. $log_{m}i$ şeklindeki logaritmanın $log_{m}i={\frac {lni}{lnm}}$ şeklinde dönüştürülerek bulunabilir. Negatif logaritmaya benzer bir şekilde Euler özdeşliğinden $i\pi =ln(-1)$ şeklinde bulunmuştu (yukarıda) denklem düzenlenirse $i={\sqrt {-1}}$ den dolayı $i\pi =ln(-1)\Rightarrow i\pi =lni^{2}\Rightarrow {\frac {i\pi }{2}}=lni$ olur. $log_{m}i={\frac {lni}{lnm}}$ denkleminde ln(i) yerine yazılırsa sonuç: $log_{m}i={\frac {i\pi }{2lnm}}$ olur.

$log_{i}m$ şeklindeki logaritma ise $log_{i}m={\frac {lnm}{lni}}$ olur. Yani $log_{i}m={\frac {1}{log_{m}i}}$ dir. $log_{m}i={\frac {i\pi }{2lnm}}$ bulunmuştu. Yerine yazılırsa $log_{i}m={\frac {1}{\frac {i\pi }{2lnm}}}$ düzenlenirse $log_{i}m={\frac {2lnm}{i\pi }}$ sonucuna ulaşılır.

Ayrıca bakınız

• Matematiksel fonksiyonların listesi

Kaynakça

• Yusuf Avcı-Nurettin Ergun-Kamil Alnıaçık. "Kolay Yoldan Logaritma" (PDF). Matematik Dünyası. 15 Mayıs 2013 tarihinde kaynağından (PDF) arşivlendi. Erişim tarihi: 6 Aralık 2013.