RC devresi
Direnç - kapasitör devresi (RC devresi) veya RC filtresi direnç ve kapsitörlerden oluşan ve gerilim veya akım kaynağı tarafından beslenen bir elektrik devresidir.
Başlangıç
[değiştir | kaynağı değiştir]Üç temel, doğrusal (lineer) analog devre elemanı vardır: direnç (R), kapasitör (C) ve bobin (L). Bunların dört önemli kombinasyonu vardır: RC devresi, RL devresi, LC devresi ve RLC devresi olarak bilinirler. Bu devreler, analog elektroniğin en önemli devrelerini oluşturur. Özellikle, pasif filtrelerde çokça kullanılır. Burada RC devresinin hem seri hem de paralel diyagramları gösteriliyor.
Karmaşık empedans
[değiştir | kaynağı değiştir]Bir kapasitörün kapasitansı C (farad) ise karmaşık empedansı ZC (ohm)
- dir.
s açısal frekans gösterir ve genellikle bir karmaşık sayıdır,
Burada
- j sanal (imajiner) birimi gösterir:
- gerçek (reel) kısım ve
- sanal kısım, yani sinüzoidal olan açısal frekans (radyan/saniye)tır.
Seri devre
[değiştir | kaynağı değiştir]
Devrede kapasitör üzerindeki gerilim:
ve direnç üzerindeki gerilim:
- dir.
Transfer fonksiyonları
[değiştir | kaynağı değiştir]Kapasitörün transfer fonksiyonu
ve aynı şekilde direncin transfer fonfsiyonu
- dir.
Kutuplar ve sıfırlar
[değiştir | kaynağı değiştir]Her iki transfer fonksiyonunda da tek kutup vardır.
- .
Ek olarak, direnç için orijinde sıfır vardır.
Kazanç ve faz açısı
[değiştir | kaynağı değiştir]Kazanç iki etkene bağlıdır: Biri
diğeri ise
- dir
ve faz açıları:
ve
- .
Bu ifadeler birlikte kullanılabilir ve genellikle fazör çıkışı temsil eder:
- .
Akım
[değiştir | kaynağı değiştir]Seri devrelerde akım her yerde aynıdır:
İmpuls cevabı
[değiştir | kaynağı değiştir]Her gerilim için impuls cevabı transfer fonksiyonunun karşılığı olan ters Laplace dönüşümüdür. Bu devre bir darbenin veya delta fonksiyonunun cevabının bir giriş gerilimine bağlı olduğunu gösterir.
Kapasitörün gerilimi için impuls cevabı
Burada u(t) Heaviside adım fonksiyonudur ve
Aynı şekilde direnç geriliminin impuls cevabı
Burada da δ(t) Dirac delta fonksiyonudur.
Frekans uzayı faktörleri
[değiştir | kaynağı değiştir]'a yaklaştıkça:
- olur.
'a yaklaştıkça:
- olur.
- .
Yukarıdaki denklemin çözümünden şu sonuç elde edilir:
veya
Bu da filtrenin orijinal gücün yarısına düşeceği frekansıdır.
'a yaklaştıkça:
- .
'a yaklaştıkça:
Zaman uzayı faktörleri
[değiştir | kaynağı değiştir]Zaman uzayını en doğru şekilde elde etmek için Laplace dönüşümünü ifade eden yukarıdaki ve yapıları kullanılır. Bu etkin dönüşümler e dönüştürülür.Adım girişi yaklaşımı yapılır. (örn. Önce yapılarak bulunur, sonra yapılır):
ve
- .

Kısmi kesir açılımları ve ters Laplace dönüşümüü:
- .
Bu eşitlikler kapasitör ve direnç üzerindeki gerilimleri sırasıyla hesaplamak içindir. Kapasitörün dolması sırasındaki eşitlikler; boşalması sırasındaki eşitliklerin tam tersidir. Bu eşitlikler şarj ve akım ilişkisi C=Q/V ve V=IR (Ohm Kanununa bakın) kullanılarak tekrar yazılabilir.
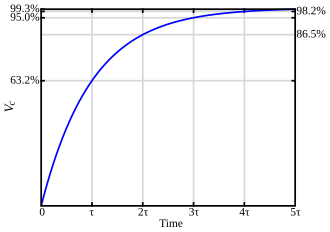
Bu eşitlikler seri RC devrelerinde bir zaman sabitinin olduğunu gösteriyor, genellikle ifadesi voltaj karşısında bileşenleri ya (C karşısında ) ya yükselir veya (R karşısında) bu son değerin ye birlikte düşer. Böylece zamanında ye ve ye ulaşabilir
Değişim oranı her bir fraksiyonel dir. Böylece, dan 'ye içinde giden voltaj bu seviyeden yolun yaklaşık 63.2 % si taşınacak de yönünde bu sonuç değerdir. Böylece C ,sonrasında yaklaşık 63.2 % ye dolacak ve yaklaşık sonrasında aslında tam dolacak (99.3 %) .Eğer voltaj kaynağı bir kısa-devre ile yerdeğiştirirse, C 0 yönünde 'den t ile C karşısında voltaj C tam yükü ile üstel şekilde damlar.C sonrasında yaklaşık 36.8 % ye düşmüş ve aslında sonrasında aslında tamamen boşalmış (0.7 %) olacak. Unutmadan akımı Ohm Kanunu yoluyla R karşısında voltaj olarak akım davranışı içinde bunu yapar
Ayrıca diferensiyel denklemler'in çözümü ile elde edilebilen bu sonuçlar devreyi tanımlayabilir:
ve
- .
İlk denklem bir integral alan faktör kullanılarak ve ikincisi takiben kolayca çözülür; çözümler böylece Laplace dönüşümleri yoluyla tam aynısı olarak elde edilir.
İntegral işlemi
[değiştir | kaynağı değiştir]yüksek frekanstada kapasitör karşısında çıkış düşünülür yani.
- .
Bunun anlamı bu kapasitörün dolmasına zaman yetersizdir ve böylece bu voltaj çok küçüktür. Böylece direnç karşısında voltaj yaklaşık giriş voltajına eşittir. için yukarıda verilen bağıntı düşünüldüğünde şuna bakalım:
ama unutmadan frekans durumu şu şekilde tanımlanır
böylece
- bu sadece Ohm kanunu'dur
Şimdi,
böylece
- ,
bu kapasitörün karşısında bir integratör'dür
Türev işlemi
[değiştir | kaynağı değiştir]düşük frekansta çıkış karşısında düşünüldüğünde; yani,
- .
Bunun anlamı bu kapasitör voltajı kadar yukarı şarja zaman var ve voltaj kaynağına neredeyse eşittir. için yine bağıntı düşünüldüğünde o zaman
- ,
böylece
Şimdi,
bu bir diferensiyatör karşısında dirençtir.
Daha kesin integrasyon ve diferansiyasyon giriş üzerinde uygun olarak dirençleri ve kapasitörler yerleştirerek ve operasyonel amplifikatörlerin döngü geribeslemesi sağlanabilir.
Paralel devre
[değiştir | kaynağı değiştir]
Paralel RC devresi genellikle seri devreden daha az ilgi görür. Çünkü çıkış gerilimi , giriş gerilimi olan e eşittir. — Sonuç olarak, bu devre bir akım kaynağı tarafından beslenen bir filtre değildir.
Karmaşık empedans:
ve
- .
Bu kapasitör akımının 90° olduğunu gösteriyor.direnç(ve kaynak) akımı ile fazın çıkışı. Karşıt olarak, diferansiyel denklemler kullanılarak yönetiliyor:
ve
- .
Bir basamak giriş için (bu etkili bir 0 Hz veya DC işaretidir), girişin türevi 'da bir uyarıdır.Böylece kapasitör çok hızlı tam yüke ulaşır ve bir açık devre olur— böylece bir kapasitörün DC davranışı iyi bilinir.
Bakınız
[değiştir | kaynağı değiştir]Dış bağlantılar
[değiştir | kaynağı değiştir]- RC Filter Calculator14 Temmuz 2011 tarihinde Wayback Machine sitesinde arşivlendi.











































































