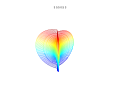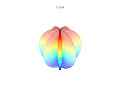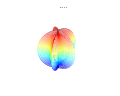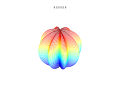Süperformül

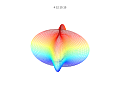
Süperformül, süperelips formülünün bir genelleştirilmesidir ve Johan Gielis tarafından 2000 yılında öne sürülmüştür. Gielis, bu formülün doğadaki birçok karmaşık şeklin ve eğrinin tanımlanmasında kullanılabileceğini söylemiştir. Gielis, süperformül ile oluşturulan bütün desenlerin patentine sahiptir.

Kutupsal koordinat sisteminde, ${\displaystyle }$ yarıçap ve ${\displaystyle }$ açı olmak üzere süperformül:

${\displaystyle }$

${\displaystyle }$

Formül, süperelips formülünün genelleştirilmesiyle elde edilmişti, ismi Danimarkalı bir matematikçi olan Piet Hein tarafından konulmuştu.

Yüksek uzantı boyutları

Formülü 3,4 veya n boyutlarında uzatmak mümkündür. Örnek olarak, 3B parametrik yüzey: r1 ve r2 formüllerini ikiye katlayarak elde edilir. Koordinatlar ilişkilerle ifade edilir:

${\displaystyle }$

${\displaystyle }$

${\displaystyle }$

(enlem) arasında −π/2 ve π/2, θ (boylam) arasında −π ve π değişir.

Genelleme

${\displaystyle }$ile y'yi ve ${\displaystyle }$ile z'yi değiştirerek genelleştirilebilir.

${\displaystyle }$

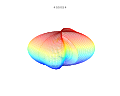
Bu formül, mantıken asimetrik ve iç içe geçmiş yapılar oluşturulmasını sağlar. Aşağıdaki örnekler a, b, ${\displaystyle }$ ve ${\displaystyle }$ 1:

Arsalar

• 
• 
• 
• 
• 
• 
• 
• 

Dış bağlantılar

• Bu superformula ve Johan Gielis hakkında bilgi 4 Ekim 2016 tarihinde Wayback Machine sitesinde arşivlendi.
• Global Optimizasyon algoritmalar tarafından Gielis eğri Uydurma bazı Deneyler ve Parçacık Sürü Yöntem
• Optimizasyonu Parçacık Sürü Yöntemi İle Chacon-Gielis eğri en küçük Kareler Uydurma
• Superformula 2D Plotter & SVG Jeneratör 31 Ekim 2009 tarihinde Wayback Machine sitesinde arşivlendi.
• Etkileşimli örnek JSXGraph kullanarak 7 Ekim 2016 tarihinde Wayback Machine sitesinde arşivlendi.
• 3D Superdupershape Explorer kullanarak İşleme 19 Ekim 2016 tarihinde Wayback Machine sitesinde arşivlendi.
• (Kod ile)etkileşimli 3D Superformula çizici kullanarak İşleme
• SuperShaper: Bir açık kaynak kodlu, hızlandırılmış OpenCL (OpenGL3)shader tabanlı görselleştirme ile 3D SuperShape jeneratör interaktif 11 Haziran 2016 tarihinde Wayback Machine sitesinde arşivlendi.
• Sade ve basit, WebGL SuperShape uygulaması
• Bu Gielis Supershape Formül 22 Eylül 2016 tarihinde Wayback Machine sitesinde arşivlendi., Sağlar interaktif bir Java uygulaması için keşfetmek çeşitli farklı şekil, doğal ya da matematiksel, olabilir oluşan formülü.