Sinc fonksiyonu

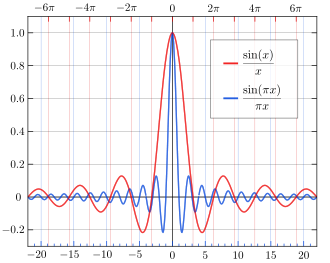
Sinc fonksiyonu matematik, fizik ve mühendislikte kullanılan bir trigonometrik fonksiyondur. Fonksiyonun normalize edilmemiş ve normalize edilmiş iki şekli vardır.

Fonksiyon

Normalize edilmemiş sinc(x) ve cos (x).

$sinc(x)={\frac {sin(x)}{x}}$

$sinc(0):=\lim _{x\to 0}{\frac {\sin(ax)}{ax}}=1$

Fonksiyon Taylor serisi ile ifade edilirse, $${\frac {\sin x}{x}}=\sum _{n=0}^{\infty }{\frac {(-1)^{n}x^{2n}}{(2n+1)!}}=1-{\frac {x^{2}}{3!}}+{\frac {x^{4}}{5!}}-{\frac {x^{6}}{7!}}+\cdots$$ $$\sum _{n=1}^{\infty }\operatorname {sinc} (n)=\operatorname {sinc} (1)+\operatorname {sinc} (2)+\operatorname {sinc} (3)+\operatorname {sinc} (4)+\cdots ={\frac {\pi -1}{2}}.$$

Bu fonksiyonun türevi,

${\frac {d}{dx}}sinc(x)={\frac {cos(x)-sinc(x)}{x}}$

Normalize edilmiş fonksiyon

Normalize ve normalize olmayan sinc (x)

$sinc(x)={\frac {sin(\pi x)}{\pi x}}$

$${\frac {\sin \pi x}{\pi x}}=1-{\frac {\pi ^{2}x^{2}}{3!}}+{\frac {\pi ^{4}x^{4}}{5!}}-{\frac {\pi ^{6}x^{6}}{7!}}+\cdots$$

Ayrıca bakınız

• Borwein integrali