Testere dişi sinyal

Testere dişi dalgası
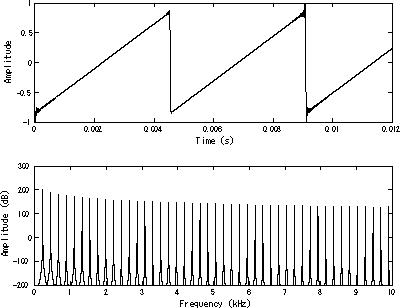Zaman ekseninde (üstte) ve frekans ekseninde (altta) resmedilen bant sınırlı bir testere dişi dalga. Temel dalga 220 Hz'de (A3).
Genel bilgiler
Genel tanım	$x(t)=2\left(t-\left\lfloor t+{\tfrac {1}{2}}\right\rfloor \right),t-{\tfrac {1}{2}}\notin \mathbb {Z}$
Uygulama alanları	Elektronik, sentezleyiciler
Tanım kümesi, değer kümesi ve görüntü kümesi
Tanım kümesi	$\mathbb {R} \setminus \left\{n-{\tfrac {1}{2}}\right\},n\in \mathbb {Z}$
Değer kümesi	$\left(-1,1\right)$
Temel özellikler
Eşlik	Tek
Periyot	1
Belirli özellikler
Kök	$\mathbb {Z}$
Fourier serisi	$x(t)=-{\frac {2}{\pi }}\sum _{k=1}^{\infty }{\frac {{\left(-1\right)}^{k}}{k}}\sin \left(2\pi kt\right)$

Şekil 1:Artan harmonik sayısı ile üretilmiş tester dişi fonksiyon (50. harmoniğe kadar)

Şekil 2:Testere dişi fonksiyon zaman ve frekans ekseninde. (Örnekte ana frekans 220 Hz. dir)

Testere dişi sinyal elektronikte genellikle ölçüm amacıyla kullanılan periodik bir sinyaldir.

Her periyotta gerilim değeri düzgün bir şekilde artar ve periyot sonunda ani olarak düşer. Aynı sinyalin tersi de kullanılabilir. Ters testere dişinde gerilim değeri periyot boyunca azalır ve periyot sonunda ani olarak artar. Testere dişi bir periyodik fonksiyon olduğundan, seri açılımıyla gösterilebilir:

$$y(t)=a\left({\frac {1}{2}}-{\frac {1}{\pi }}\sum _{k=1}^{\infty }{(-1)}^{k}{\frac {\sin(2\pi kft)}{k}}\right)$$

Burada a genlik ve p periyodu göstermektedir. Ana frekans ise;

$$f={\frac {1}{p}}$$

Şekil 1,2deki animasyonda tek bir sinüs sinyalinden başlayarak, artan sayıda terim kullanılarak, oluşturulan bir testere dişi fonksiyon gösterilmektedir. 2.şekilde ise bir testere dişi hem zaman, hem de frekans ekseninde gösterilmiştir.

Ters testere dişi fonksiyonun seri açılımı ise;

$$y_{\text{ters}}(t)={\frac {2a}{\pi }}\sum _{k=1}^{\infty }{(-1)}^{k}{\frac {\sin(2\pi kft)}{k}}$$

Doğrusallık ölçümü

Testere dişi sinyal en çok doğrusallık ölçümü için kullanılır. Doğrusallığı ölçülecek cihaz girişine testere dişi sinyal uygulanır. Çıkış bir osiloskopta incelenir. Çıkışın da testere dişi olması gerekir. Şayet testere dişi sinyalde bozulma varsa bu cihazın doğrusal olmadığını gösterir.