Dönel cisim

Eğri döndürülüyor. Cismi çevreleyen bu yüzey dönel yüzeydir.

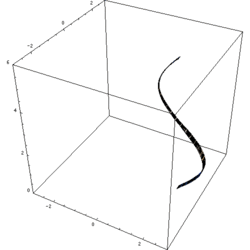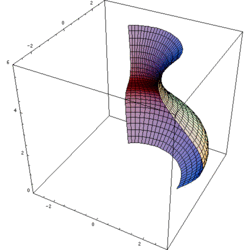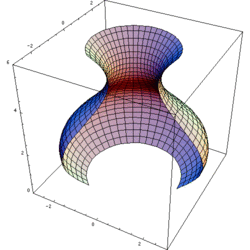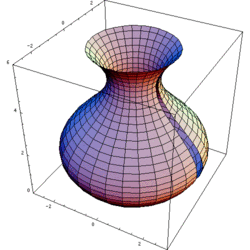
Matematik, mühendislik ve imalat alanlarında kullanılan dönel cisim, bir eğriyi aynı düzlemde bulunan bir doğru (dönme ekseni) etrafında döndürülerek elde edilen şekildir.

Eğrinin dönme eksenini geçmediği kabul edilirse; dönel cismin hacmi, şeklin ağırlık merkezini merkez kabul eden dairenin uzunluğu ile şeklin alanının çarpımıdır (Pappus'un Ağırlık Merkezi Teoremi).

Temsili disk dönel cisimin üç-boyutlu bir hacim elemanıdır. Bu eleman (w uzunluğunda) bir doğru parçasının (r birim uzaklıkta) bir eksen etrafında döndürülmesiyle oluşturulur. Böylece πr²w birimlik silindirik hacim çevrelenmiş olur.

Hacim bulma

Dönel cismin hacmini bulmak için sıklıkla kullanılan iki integrasyon yöntemi, disk yöntemi ve kabuk yöntemidir. Bu yöntemleri uygulamak için, grafik çizmek en kolayıdır; dönme ekseni etrafında döndürülecek alan belirlenir; dönel cismin δx kalınlığına sahip disk şeklindeki bir diliminin ya da δx genişliğindeki silindirik bir kabuğun hacmi bulunur ve bu hacimlerin δx 0'a yakınsarkenki limit toplamı hesaplanır. Bu limit değeri, uygun bir integral hesaplanarak da bulunabilir.

Disk yöntemi

Y-ekseni etrafında disk integrasyonu

Ana madde: Disk integrasyonu

Disk yöntemi, çizilen dilimin dönme eksenine dik olduğu zaman yani dönme eksenine paralel integrasyon gerçekleştirilirken kullanılır.

$f(x)$ ve $g(x)$ eğrileri ve $x=a$ ve $x=b$ doğruları arasında kalan alan x-ekseni etrafında döndürülerek oluşan dönel cismin hacmi şöyle ifade edilir:

$V=\pi \int _{a}^{b}\vert f^{2}(x)-g^{2}(x)\vert \,dx$

Eğer g(x) = 0 ise (yani bir eğri ile x-ekseni arasındaki alan döndürülüyorsa) formül şöyle indirgenir:

$V=\pi \int _{a}^{b}f^{2}(x)\,dx\qquad (1)$

Bu yöntem üst noktası $f(y)$ alt noktası $g(y)$ olmak üzere yatay olarak uzanan çok ince bir dikdörtgen ile görselleştirilebilir. Bu dikdörtgen y-ekseni etrafında döndürülürse yüzük biçimini alır ($g(y)=0$ ise disk olur). Bu yüzüğün dış yarıçapı f(y) iç yarıçapı ise g(y) olur. R dış yarıçap (bu durumda f(y)), r iç yarıçap (bu durumda g(y)) olmak üzere bu yüzüğün alanı $\pi (R^{2}-r^{2})$ dir. Aralıktaki tüm alanları toplamak toplam hacmi verir. Bu yüzden her bir sonsuz küçük diskin hacmi $\pi f^{2}(x)dx$ dir. Bu disklerin a ve b aralığındaki sonsuz toplamı açıkça integral (1) şeklinde kendini gösterir.

Silindir yöntemi

Kabuk integrasyonu

Ana madde: Kabuk integrasyonu

Silindir yöntemi, çizilen dilimin dönme eksenine paralel olduğu zaman yani dönme eksenine dik integrasyon gerçekleştirilirken kullanılır.

$f(x)$ ve $g(x)$ eğrileri ve $x=a$ ve $x=b$ doğruları arasında kalan alan y-ekseni etrafında döndürülerek oluşan dönel cismin hacmi şöyle ifade edilir:

$V=2\pi \int _{a}^{b}x\vert f(x)-g(x)\vert \,dx$

Eğer g(x) = 0 ise (yani bir eğri ile x-ekseni arasındaki alan döndürülüyorsa) formül şöyle indirgenir:

$V=2\pi \int _{a}^{b}x\vert f(x)\vert \,dx$

Bu yöntem $[f(x)-g(x)]$ yüksekliğine sahip ve dikey olarak uzanan çok ince bir dikdörtgen ile görselleştirilebilir. Bu dikdörtgen y-ekseni etrafında döndürülürse silindirik kabuk biçimini alır. r yarıçap (bu durumda x) h yükseklik (bu durumda $[f(x)-g(x)]$) olmak üzere bir silindirin yanal alanı $2\pi rh$ dir. Aralıktaki tüm yüzey alanlarını toplamak toplam hacmi verir.

Parametrik form

Bir eğri $(x(t),y(t))$ parametrik formunda $[a,b]$ aralığında tanımlandığında, eğriyi x-ekseni veya y-ekseni etrafında döndürülerek oluşturulan dönel cisimlerin hacmi şöyle verilir:

$V_{x}=\int _{a}^{b}\,\pi \,y^{2}\,{\frac {dx}{dt}}\,dt$

$V_{y}=\int _{a}^{b}\pi \,\,x^{2}\,{\frac {dy}{dt}}\,dt.$

Aynı şartlar altında eğriyi x-ekseni veya y ekseni etrafında döndürülerek oluşturulan dönel cisimlerin yüzey alanları şöyle verilir:

$A_{x}=\int _{a}^{b}2\pi y\,{\sqrt {\left({\frac {dx}{dt}}\right)^{2}+\left({\frac {dy}{dt}}\right)^{2}}}\,dt$

$A_{y}=\int _{a}^{b}2\pi x\,{\sqrt {\left({\frac {dx}{dt}}\right)^{2}+\left({\frac {dy}{dt}}\right)^{2}}}\,dt$

Kaynakça

• CliffsNotes.com. Volumes of Solids of Revolution. 12 Apr 2011 <https://web.archive.org/web/20120319195953/http://www.cliffsnotes.com/study_guide/topicArticleId-39909,articleId-39907.html>.
• Frank Ayres, Elliott Mendelson. Schaum's Outlines: Calculus. McGraw-Hill Professional 2008, ISBN 978-0-07-150861-2. pp. 244–248 (Google Kitaplar'da online copy, s. 244,)
• Eric W. Weisstein, Solid of Revolution (MathWorld)
• Vikipedi Solid of revolution makalesi. (Son Erişim Tarihi: 05.04.2015)