Gabor Filtresi

Bir iki boyutlu Gabor Filtresi örneği

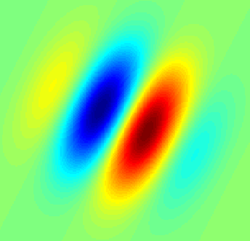
Bir Gabor filtresi, harmonik bir fonksiyon ile Gaussian bir fonksiyonunun çarpımından oluşan lineer bir filtredir.

$g(x,y;\lambda ,\theta ,\psi ,\sigma ,\gamma )=\exp \left(-{\frac {x'^{2}+\gamma ^{2}y'^{2}}{2\sigma ^{2}}}\right)\cos \left(2\pi {\frac {x'}{\lambda }}+\psi \right)$

ki

$x'=x\cos \theta +y\sin \theta \,$

ve

$y'=-x\sin \theta +y\cos \theta \,$

Bu denklemde, $\lambda$ kosinüsün dalgaboyu faktörünü, $\theta$ Gabor fonksiyonunun yönünü, $\psi$ fazın ofset değerini ve $\gamma$ ise de uzamsal görüş açısını belirtir.

Farklı yönelimli Gabor filtereleri hedef görüntü ile katlanarak ve bu görüntülerin ortalamaları alınarak hedef görüntüdeki farklı açı bileşenleri ortaya çıkarılabilir.Gabor uzayı iris tanıma, yüz tanıma gibi görüntü işleme uygulamalarında kullanılır.

Ayrıca bakınız

• Dennis Gabor

Dış bağlantılar

2 boyutlu Gabor filtreleri ve bazı resimlerle katlandıktan sonraki oluşan görüntüleri görebilmek için https://web.archive.org/web/20090615224334/http://matlabserver.cs.rug.nl/ adresi faydalı bir kaynaktır.