Hipotrokoid

Kırmızı eğri, küçük siyah çember büyük mavi çemberin içinde yuvarlanırken çizilen bir hipotrokoiddir (parametreler R = 5, r = 3, d = 5).

Geometride hipotrokoid, R yarıçaplı sabit bir çemberin içinde yuvarlanan r yarıçaplı bir çembere bağlı olan bir nokta tarafından izlenen bir yuvarlanma eğrisidir, burada nokta iç çemberin merkezinden d kadar bir mesafededir.

Bir hipotrokoid için parametrik denklemler şu şekildedir:

${\begin{aligned}&x(\theta )=(R-r)\cos \theta +d\cos \left({R-r \over r}\theta \right)\\&y(\theta )=(R-r)\sin \theta -d\sin \left({R-r \over r}\theta \right)\end{aligned}}$

burada θ yatay ile yuvarlanan dairenin merkezinin oluşturduğu açıdır (bunlar kutupsal denklemler değildir çünkü θ kutupsal açı değildir). Radyan cinsinden ölçüldüğünde, θ 0 ile $2\pi \times {\tfrac {\operatorname {EKOK} (r,R)}{R}}$ arasında değerler alır (burada EKOK, en küçük ortak katı ifade eder).

Özel durumlar arasında d = r ile hiposikloid ve R = 2r ve d ≠ r ile elips bulunur. Elipsin eksantrikliği şöyledir:

$e={\frac {2{\sqrt {d/r}}}{1+(d/r)}}$

$d=r$ olduğunda bu değer 1 olur (bkz. Tusi çifti).

Elips (kırmızı ile çizilmiştir), R = 2r (Tusi çifti) ile hipotrokoidin özel bir durumu olarak ifade edilebilir; burada R = 10, r = 5, d = 1.

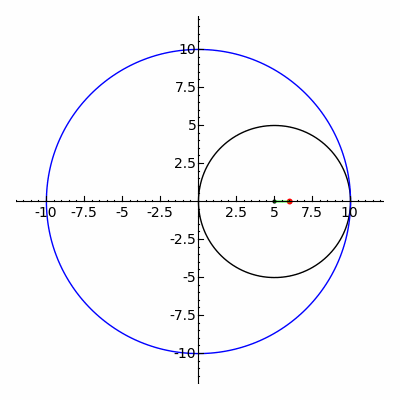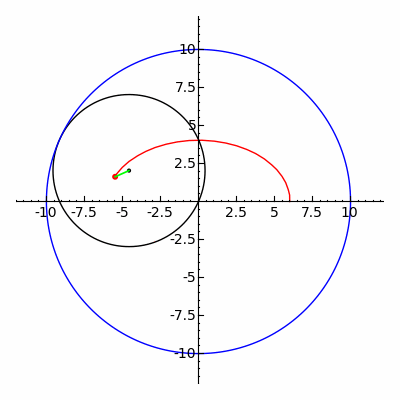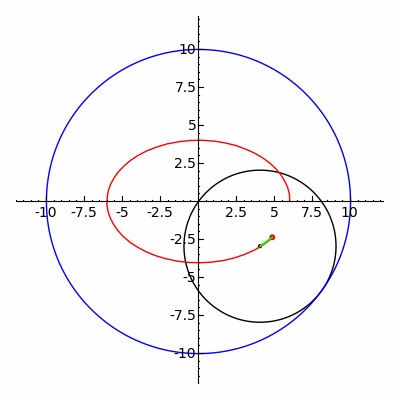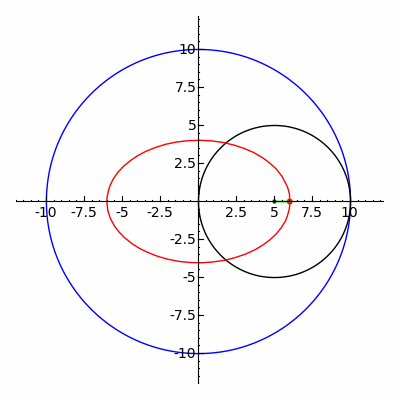
Klasik spirograf oyuncağı, hipotrokoid ve epitrokoid eğrilerinin izini sürer.

Hipotrokoidler, döngüsel korelasyonlara sahip bazı rastgele matrislerin özdeğerlerinin desteğini tanımlar.

Ayrıca bakınız

• Sikloid
• Siklogon
• Episikloid
• Rosetta (yörünge)
• Kubbemsi yalpalanma
• Spirograf

Dış bağlantılar

• Eric W. Weisstein, Hypotrochoid (MathWorld)
• Flash Animation of Hypocycloid
• Hypotrochoid from Visual Dictionary of Special Plane Curves, Xah Lee
• Interactive hypotrochoide animation
• O'Connor, John J.; Robertson, Edmund F., "Hypotrochoid", MacTutor Matematik Tarihi arşivi