Belirsiz form

Kalkülüs ve matematiksel analizin diğer dallarında cebirsel işlemlerle ilgili olan limitler, daha çok alt ifadelerin yer değiştirmesi ile gerçekleştirilir. Bu değişimden sonra elde edilen ifade eğer, asıl limit ile ilgili yeteri kadar bilgi içermiyorsa, buna 'belirsiz form denir.

Bilinen en yaygın belirsiz formlar, 0/0, ∞/∞, 0 × ∞, ∞ × 0, ∞ − ∞, 0⁰, 1^∞ ve ∞⁰ dir.

Tartışma

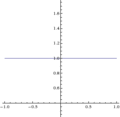
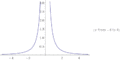
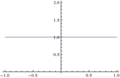
Belirsiz formun en yaygın bilinen örneği, iki fonksiyonun oranında ortaya çıkar. Bu iki fonksiyonun limiti sıfıra eğilimlidir ve "0/0 belirsiz formu" olarak ifade edilir. x, 0'a yaklaşırken, x/x³, x/x ve x²/x oranları sırasıyla ∞, 1 ve 0'a yaklaşır. Her bir durumda eğer pay ve paydanın limitleri yerine konulursa, sonuçta 0/0 ifadesi elde edilir. Böylece 0/0, 0, 1 veya ∞ değerlerini alabilir.

Daha formal bir ifade ile, f(x) ve g(x) fonksiyonları 0'a yaklaşır. Burada xin bazı c limit noktasına yaklaşması, limit hakkında yeterli bilgi içermediği anlamına gelir.

$\lim _{x\to c}{\frac {f(x)}{g(x)}}.\!$

Belirsiz form cebirsel ifadelerin tümü ile tanımlı değildir. Örneğin 1/0 ifadesi, reel sayılarda tanımsızdır. Fakat bu, belirsiz form olduğu anlamına gelmez. Çünkü bu formun herhangi bir limiti, sonsuza ıraksar.

Bazı örnekler ve örneksizler

0/0 belirsiz formu

• 
  (1)
• 
  (2)
• 
  (3)
• 
  (4)
• 
  (5)
• 
  (6)

0/0 belirsiz formuna kalkülüsde sıkça rastlanır. Limit tanımları kullanılarak türevlerinin değerleri elde edilebilir.

$\lim _{x\to 0}{\frac {x}{x}}=1,\!~~(1)$

while

$\lim _{x\to 0}{\frac {x^{2}}{x}}=0,\!~~(2)$

Bu, 0/0 ifadesinin belirsiz form olduğunu göstermek için yeterlidir. Bu belirsiz forma diğer örnekler şunlardır:

$\lim _{x\to 0}{\frac {\sin(x)}{x}}=1,\!~~(3)$

ve

$\lim _{x\to 49}{\frac {x-49}{{\sqrt {x}}\,-7}}=14,~~(4)$

$\lim _{x\to 0}{\frac {ax}{x}}=a.\!~~(5)$

The value infinity can also be obtained (in the sense of divergence to infinity):

$\lim _{x\to 0}{\frac {x}{x^{3}}}=\infty .\!~~(6)$

0⁰ belirsiz formu

• 
  (7)
• 
  (8)

Aşağıda 0⁰ belirsiz formuna örnekler verilmiştir:

$\lim _{x\to 0^{+}}x^{0}=1,\!~~(7)$

$\lim _{x\to 0^{+}}0^{x}=0.\!~~(8)$

Burada genellikle $\scriptstyle \lim _{x\to c}f(x)\;=\;0^{+}\!$ ve $\scriptstyle \lim _{x\to c}g(x)\;=\;0$'ın bilinmesi aşağıdaki limit hesaplamak için yeterli değildir:

$\lim _{x\to c}f(x)^{g(x)}.$

Belirsiz formlar listesi

Aşağıdaki tabloda, sıkça rastlanan belirsiz formlar ve l'Hôpital's kuralı ile yapılan dönüşümleri listelenmiştir.

Belirsiz form	Şartlar	0/0 dönüşümü	∞/∞ dönüşümü
0/0	$\lim _{x\to c}f(x)=0,\ \lim _{x\to c}g(x)=0\!$	—	$\lim _{x\to c}{\frac {f(x)}{g(x)}}=\lim _{x\to c}{\frac {1/g(x)}{1/f(x)}}\!$
∞/∞	$\lim _{x\to c}f(x)=\infty ,\ \lim _{x\to c}g(x)=\infty \!$	$\lim _{x\to c}{\frac {f(x)}{g(x)}}=\lim _{x\to c}{\frac {1/g(x)}{1/f(x)}}\!$	—
0 × ∞	$\lim _{x\to c}f(x)=0,\ \lim _{x\to c}g(x)=\infty \!$	$\lim _{x\to c}f(x)g(x)=\lim _{x\to c}{\frac {f(x)}{1/g(x)}}\!$	$\lim _{x\to c}f(x)g(x)=\lim _{x\to c}{\frac {g(x)}{1/f(x)}}\!$
∞ − ∞	$\lim _{x\to c}f(x)=\infty ,\ \lim _{x\to c}g(x)=\infty \!$	$\lim _{x\to c}(f(x)-g(x))=\lim _{x\to c}{\frac {1/g(x)-1/f(x)}{1/(f(x)g(x))}}\!$	$\lim _{x\to c}(f(x)-g(x))=\ln \lim _{x\to c}{\frac {e^{f(x)}}{e^{g(x)}}}\!$
00	$\lim _{x\to c}f(x)=0^{+},\lim _{x\to c}g(x)=0\!$	$\lim _{x\to c}f(x)^{g(x)}=\exp \lim _{x\to c}{\frac {g(x)}{1/\ln f(x)}}\!$	$\lim _{x\to c}f(x)^{g(x)}=\exp \lim _{x\to c}{\frac {\ln f(x)}{1/g(x)}}\!$
1∞	$\lim _{x\to c}f(x)=1,\ \lim _{x\to c}g(x)=\infty \!$	$\lim _{x\to c}f(x)^{g(x)}=\exp \lim _{x\to c}{\frac {\ln f(x)}{1/g(x)}}\!$	$\lim _{x\to c}f(x)^{g(x)}=\exp \lim _{x\to c}{\frac {g(x)}{1/\ln f(x)}}\!$
∞0	$\lim _{x\to c}f(x)=\infty ,\ \lim _{x\to c}g(x)=0\!$	$\lim _{x\to c}f(x)^{g(x)}=\exp \lim _{x\to c}{\frac {g(x)}{1/\ln f(x)}}\!$	$\lim _{x\to c}f(x)^{g(x)}=\exp \lim _{x\to c}{\frac {\ln f(x)}{1/g(x)}}\!$