Momentum

Klasik mekanikte momentum ya da devinirlik (çoğul momenta; SI birimi kg·m/s ya da eşdeğer olarak, N·s), bir nesnenin kütlesi ve hızının çarpımıdır; (p = mv). Hız gibi, momentum da vektörel bir niceliktir, yani büyüklüğünün yanı sıra bir yöne de sahiptir. Momentum korunumlu bir niceliktir (çizgisel momentumun korunumu); yani bu, eğer kapalı bir sistem herhangi bir dış kuvvetin etkisi altında değilse, o kapalı sistemin toplam momentumunun değişemeyeceği anlamına gelir. Momentum benzer bir konu olan açısal momentum ile karışmasın diye, bazen çizgisel momentum olarak da anılır.

Her ne kadar Newton'un ikinci yasası şeklinde ifade edilse de, momentumun korunumu Özel görelilik teorisi çerçevesi içinde de geçerlidir ve bazı uygun tanımlarla birlikte, (genelleştirilmiş) bir momentum korunum yasası Elektrodinamik, kuantum mekaniği, kuantum alan teorisi ve genel görelilik teorileri içinde de geçerliliğini korur. Göreli mekanikteki momentum, göreli-olmayan momentumun, fazladan Lorentz faktörü ile çarpılmasıyla elde edilir.

Bir parçacığın çizgisel momentumu

Einstein'ın asansöründeki Newton'un elması. A kişisinin gözlem çerçevesinde, elma sıfır olmayan bir hıza ve momentuma sahiptir. Asansörün ve B kişisinin gözlem çerçevesinde ise, elma, sıfır bir hıza ve momentuma sahiptir.

Bir nesne herhangi bir gözlem çerçevesinde hareket halinde ise, o çerçeve içinde bir momentuma sahiptir. Momentumun çerçeveye bağımlı olduğunu belirtmek önemlidir. Yani aynı nesne, bir gözlem çerçevesinde belli bir momentum değerine sahip olabilirken, başka bir gözlem çerçevesinde ise başka bir momentum değerine sahip olabilir. Örneğin, hareketli bir nesne, yere göre sabit bir noktaya göre seçilen bir gözlem çerçevesinde momentumu olmasına rağmen, kütle merkezine iliştirilen bir gözlem çerçevesinde ise sıfır momentumu vardır.

Bir nesnenin sahip olduğu momentumun miktarı, iki fiziksel büyüklüğe bağlıdır: Kütlesi ve o gözlem çerçevesindeki hızı. Fizikte, momentum için kullanılan sembol genellikle kalın p harfidir (kalın yazılmasının nedeni vektör olmasındandır.); böylece şöyle ifade edilebilir;

$\mathbf {p} =m\mathbf {v} \,,$

burada p momentum, m kütle ve v hızdır.

Örnek: kuzeye doğru yere paralel düz bir rotada 1 m/s hızına ve 1 kg kütleye sahip model bir uçağın momentumu yere göre ölçüldüğünde, kuzey yönünde 1 kg•m/s 'dir. Kokpitin içindeki bir pilot, kokpit gözlem çerçevesine göre uçağın hızını sıfır ölçeceğinden, momentumunu da sıfır ölçer.

Newton'un ikinci yasasına göre, bir parçacığın momentumunun değişim hızı, parçacık üzerine etki eden net kuvvetle doğru orantılıdır ve yönü ise bu net kuvvetin yönündedir. Net kuvvetin, momentumdan türetilmesi aşağıdaki gibidir.

$\sum {\mathbf {F} }={\mathrm {d} \mathbf {p} \over \mathrm {d} t}=m{\mathrm {d} \mathbf {v} \over \mathrm {d} t}+\mathbf {v} {\mathrm {d} m \over \mathrm {d} t}$

Eğer kütle zaman içinde sabitse, türevin ikinci terimi (thrust terimi denir) ($\scriptstyle \mathbf {v} {\mathrm {d} m \over \mathrm {d} t}=0$). Böylece şunu yazabiliriz:

$\sum {\mathbf {F} }=m\mathbf {a} \,$

Ya da daha basit olarak,

$\mathbf {F} =m\mathbf {a} \,,$

burada F'nin net kuvvet olduğu anlaşılmalıdır.

Örnek: yine bir model uçak, 1 kg kütleli, 1 s içinde kuzeye doğru sıfır hızdan 1 m/s hızına ivmelensin. Bu ivmelenme için gerekli kuvvet 1 newtondur. Momentumdaki değişim 1 kg•m/s'dir. Kokpitteki pilot için ise momentumda bir değişim yoktur. İvmelenme sırasında pilotun sırtının koltuğa yapışması, bu itme'ye tepki kuvvetine karşı dengelenmedir.

Birçok-parçacık sisteminin çizgisel momentumu

Kütle ve hız bağıntıları

Çok-parçacık sisteminin çizgisel momentumu, sistem içindeki ayrı ayrı tüm nesnelerin momentumlarının vektörel toplamlarına eşittir.

$\mathbf {p} =\sum _{i=1}^{n}m_{i}\mathbf {v} _{i}=m_{1}\mathbf {v} _{1}+m_{2}\mathbf {v} _{2}+m_{3}\mathbf {v} _{3}+\cdots +m_{n}\mathbf {v} _{n}\,,$

burada p' parçacık sisteminin toplam momentumu, mi vevi iinci nesnenin sırasıyla kütlesi ve hızı ve n ise sistemdeki nesnelerin sayısıdır..

Gösterilebilir ki, kütle merkezi çerçevesinde herhangi bir sistemin momentumu sıfırdır. Dahası, bu kütle merkezi çerçevesine göre hızı v_km olan başka bir çerçevedeki momentum basitçe aşağıdaki gibidir:

$\mathbf {p} =m\mathbf {v} _{\text{km}}\,,$

burada:

$m=\sum _{i=1}^{n}m_{i}\,.$

Bu Euler'in ilk yasası olarak bilinir.

Kuvvet bağıntısı – Genel hareket denklemleri

Maddesel bir gövdenin hareketi

Birçok-parçacıklı sistemin çizgisel momentumu, toplam kütle m ile kütle merkezi hızı v_km'nin çarpımı olarak da tanımlanabilir.

$\sum {\mathbf {F} }={\mathrm {d} \mathbf {p} \over \mathrm {d} t}=m{\frac {\mathrm {d} \mathbf {v} _{km}}{\mathrm {d} t}}=m\mathbf {a} _{km}\,$

Bu Newton'un ikinci yasasının özel bir halidir (eğer kütle sabitse).

Tensörler kullanılarak yapılacak daha genel bir türetim için, bir t anında, V hacmini kaplayan, bir S yüzey alanına sahip, stres vektörü $\scriptstyle T_{i}^{(n)}\,$ ile temsil edilen birim yüzey alanı başına yüzey kuvvetinin ettiği, V hacmi içinde her noktadaki birim hacim başına olan F_i gövde kuvvetinin etkidiği, cismin gövdesi boyunca belirlenmiş v_i hız alanı ile belirlenmiş, sürekli bir ortam olduğu varsayılan, hareket halindeki bir cismi düşünelim(şekle bakın).

$\int _{S}T_{i}^{(n)}dS+\int _{V}F_{i}dV={\frac {d}{dt}}\int _{V}\rho \,v_{i}\,dV\,.$

Tanım gereği stres vektörü $\scriptstyle T_{i}^{(n)}\equiv \sigma _{ij}n_{j}\,$'dir, o halde

$\int _{S}\sigma _{ij}n_{j}\,dS+\int _{V}F_{i}\,dV={\frac {d}{dt}}\int _{V}\rho \,v_{i}\,dV\,.$

Gauss'un diverjans teoremini kullanarak, yüzey integrali hacim integraline çevrilirse, (burada $\scriptstyle \partial _{j}\equiv {\frac {\partial }{\partial x_{j}}}\,$ ile diferansiyel işlemci belirtilmektedir), bu bize şunu verir:

$\int _{V}\partial _{j}\sigma _{ij}\,dV+\int _{V}F_{i}\,dV={\frac {d}{dt}}\int _{V}\rho \,v_{i}\,dV\,.$

Artık sadece bu eşitliğin sağ tarafıyla ilgilenebiliriz. Bu noktada dikkat etmemiz gereken, diferansiyel işlemciyi sadece integranda uygulamamaktır. Çünkü bu sürekli ortama sahip gövdenin hareketi esnasında, gövde katı bir cisim olmak zorunda olmadığından, integre ettiğimiz hacim de zaman içinde değişebilir. O halde yukarıdaki integral şu hali alır:

${\frac {d}{dt}}\int \rho \,v_{i}\,dV=\int {\frac {\partial (\rho v_{i})}{\partial t}}\,dV+\oint \rho v_{i}v_{k}n_{k}dA\,.$

Birinci kısımda türev alınır ve ikinci kısma diverjans teoremi uygulanırsa:

${\frac {d}{dt}}\int \rho \,v_{i}\,dV=\int \left[\left(\rho {\frac {\partial v_{i}}{\partial t}}+v_{i}{\frac {\partial \rho }{\partial t}}\right)+\partial _{k}(\rho v_{i}v_{k})\right]\,dV\,.$ elde edilir.

Artık integralin içindeki ikinci terim şudur: $\partial _{k}(\rho v_{i}v_{k})=\rho v_{k}\cdot \partial _{k}v_{i}+v_{i}\partial _{k}(\rho v_{k})\,.$ Bunu önceki denklemde yerine koyup, terimleri düzenledikten sonra, şunu elde ederiz:

${\frac {d}{dt}}\int \rho \,v_{i}\,dV=\int \rho \left[{\frac {\partial }{\partial t}}+v_{k}\partial _{k}\right]v_{i}\,dV+\int \left[{\frac {\partial \rho }{\partial t}}+\partial _{k}(\rho v_{k})\right]v_{i}\,dV\,.$

Yukarıdaki denklemlerdeki iki integral terimini kolayca tanıyabiliriz. İlk integral hız alanının konvektif türevini ve ikinci integral ise kütlenin zaman içindeki akışını ve değişimini ihtiva eder. Şimdi ise sistemde ne bir kaynak (source) ne de bir gider (sink) olduğunu varsayalım, yani kütle korunuyor olsun, o halde bu ikinci terim sıfırdır. Böylece şunu elde ederiz:

${\frac {d}{dt}}\int \rho \,v_{i}\,dV=\int \rho \,{\frac {Dv_{i}}{Dt}}\,dV\,$

Bunu orijinal denkleme geri koyarsak:

$\int _{V}\left[\partial _{j}\sigma _{ij}+F_{i}-\rho {\frac {Dv_{i}}{Dt}}\right]\,dV=0\,.$

Herhangi bir hacim için integrand sıfır olması gerektiğinden, Cauchy hareket denklemlerini elde ederiz

$\partial _{j}\sigma _{ij}+F_{i}=\rho {\frac {Dv_{i}}{Dt}}\,.$

Görüldüğü gibi bunu elde etmek için sadece hiçbir kütle kaynağı veya kütle giderinin olmadığını, yani kütlenin korunduğu varsayımını yaptık. O halde bu denklem herhangi bir sürekli sistem için, akışkan sistemlerde dahi geçerlidir. Eğer yalnızca elastic sürekliliği inceliyorsak, konvektif türevin ikinci terimi ihmal edilebilir ve bu durumda bize hız alanının sıradan zaman türevi kalır. Bir sistem dengede ise, ivmesi olmayacağından, momentumunun zamana göre değişimi sıfırdır.

$\sum {\mathbf {F} }={\mathrm {d} \mathbf {p} \over \mathrm {d} t}=\ m\mathbf {a} _{cm}=0\,.$

Ya da tensör gösterimiyle,

$\partial _{j}\sigma _{ij}+F_{i}=0\,.$

Bunlar, çizgisel elastisite problemlerini çözmek için katılar mekaniğinde kullanılan denge denklemleridir. Mühendislik gösteriminde, denge denklemleri kartezyen koordinatlarda şöyle ifade edilirler:

${\frac {\partial \sigma _{x}}{\partial x}}+{\frac {\partial \tau _{yx}}{\partial y}}+{\frac {\partial \tau _{zx}}{\partial z}}+F_{x}=0\,$

${\frac {\partial \tau _{xy}}{\partial x}}+{\frac {\partial \sigma _{y}}{\partial y}}+{\frac {\partial \tau _{zy}}{\partial z}}+F_{y}=0\,$

${\frac {\partial \tau _{xz}}{\partial x}}+{\frac {\partial \tau _{yz}}{\partial y}}+{\frac {\partial \sigma _{z}}{\partial z}}+F_{z}=0\,.$

Çizgisel momentumun korunumu

Çizgisel momentumun korunumu doğanın temel bir yasası olup, eğer kapalı bir sisteme etkiyen hiçbir dış kuvvet mevcut değilse, o kapalı sistemin momentumunun sabit kalacağını söyler. Bu yasanın sonuçlarından bir tanesi ise; herhangi bir nesneler sisteminin kütle merkezi, sistem dışı bir kuvvete maruz kalmadığı sürece, her zaman aynı bir hız ile hareketini sürdürecektir.

Momentumun korunumu, matematiksel bir özellik olan uzayın homojen olmasının bir sonucudur (bir nesnenin uzay içindeki konumu, momentumuna kanonik olarak eşleniktir). O halde momentumun korunduğu bir sistemin içinde fiziksel olarak ne olup bittiği, o sistemin uzaydaki konumunun nerede olduğu ile bir ilgisi bulunmamaktadır.

Analitik mekanikte momentumun korunumu, Lagranjiyenin, ötelemeler altında değişmez kalmasının bir sonucudur. Toplam momentumun hareket sabiti olduğu, Lagranjiyene sonsuz küçük bir öteleme yapılıp, bunu ötelenmemiş Lagranjiyenle eşitlenerek ispatlanabilir. Bu Noether teoreminin özel bir halidir.

Kapalı bir sistem için (eğer dış kuvvetler yoksa) toplam momentumun korunumu aslında, Newton'un birinci hareket yasasıdır. Newton'un üçüncü yasası olan, alt sistemler arasında etkiyen kuvvetlerin büyüklükleri aynı ve yönleri zıttır şeklinde ifade edilen, etkiye tepki yasası ise momentum korunumunun bir sonucudur.

Uzaydaki konum, vektörel bir nicelik olduğundan, konuma kanonik eşlenik olan momentum da vektörel bir niceliktir-bir yöne sahiptir. O halde, bir silah ateşlendiğinde, sistemin (silah ve merminin) toplam momentumu, bu iki cismin momentumlarının vektörel toplamlarıdır. Ateşlemeden hemen öncesinde silah ve merminin duruyor oldukları farzedilirse (ki bu sistemin başlangıç momentumunun sıfır olmasıdır), sistemin son toplam momentumu da sıfır olmalıdır. Sadece iki nesneye sahip kapalı bir sistemde, nesnelerden birindeki momentum değişimi, diğerinkine büyüklük olarak eşit ve yön olarak ters olmalıdır. Matematiksel olarak,

$\Delta \mathbf {p} _{1}=-\Delta \mathbf {p} _{2}\,.$

Momentum, yine kapalı bir sistemde, çarpışmalarda ve iç patlamaların sebep verdiği ayrılmalarda dahi korunur. Kinetik enerji, öte yandan, çarpışmalar esnek değilse, korunmaz. Momentum korunduğundan dolayı, bu bir çarpışma ya da ayrılmayı takip eden durumda bilinmeyen bir hızı, eğer diğer kütle ve hızların bilinmesi durumunda, hesap edilebilir.

Bu gerçeğin gerekli olduğu, fizikte sık rastlanan bir problem, iki parçacığın çarpışmalarıdır. Momentum her zaman korunuyor olacağından, çarpışma öncesi momenta toplamı, çarpışma sonrası momenta toplamına eşit olmalıdır:

$m_{1}\mathbf {u} _{1}+m_{2}\mathbf {u} _{2}=m_{1}\mathbf {v} _{1}+m_{2}\mathbf {v} _{2}\,,$

Burada; "$\mathbf {u} _{1}\,$" ve "$\mathbf {u} _{2}\,$": Çarpışma öncesi hızlar, ${\frac {metre}{saniye}}$ biriminde. "$\mathbf {v} _{1}\,$" ve "$\mathbf {v} _{2}\,$": Çarpışma sonrası hızlar, ${\frac {metre}{saniye}}$ biriminde. "$m\,$": Kütle, ${kg}\,$ biriminde.

İlk hızlardan, son hızların belirlenmesi (ya da tam tersi), çarpışmanın çeşidine bağlıdır. İki çeşit momentum koruyan çarpışma vardır: Kinetik enerjiyi de koruyan esnek çarpışmalar ve kinetik enerjiyi korumayan esnek olmayan çarpışmalar.

Esnek çarpışmalar

İki bilardo topunun çarpışması, sertliklerinin yüksek olmasından dolayı, “neredeyse” tamamen esnek bir çarpışmaya örnek olarak verilebilir. Tamamen esnek olan çarpışmalar sadece teoride, sertlikleri matematiksel olarak sonsuz olan iki cisim arasında var olabilir. İki topun çarpışması esnasında momentumun korunmasının yanı sıra, çarpışma öncesi kinetik enerjilerin toplamı, çarpışma sonraki toplama eşit olmalıdır:

${\tfrac {1}{2}}m_{1}u_{1}^{2}+{\tfrac {1}{2}}m_{2}u_{2}^{2}={\tfrac {1}{2}}m_{1}v_{1}^{2}+{\tfrac {1}{2}}m_{2}v_{2}^{2}\,.$

Bir boyutta

Bir Newton beşiği , momentum korunumunu gösteriyor.

Başlangıç hızları bilindiğinde, kafa-kafaya olan çarpışmalardaki son hızlar şöyle verilir:

$\mathbf {v} _{1}=\left({\frac {m_{1}-m_{2}}{m_{1}+m_{2}}}\right)\mathbf {u} _{1}+\left({\frac {2m_{2}}{m_{1}+m_{2}}}\right)\mathbf {u} _{2}\,$

$\mathbf {v} _{2}=\left({\frac {m_{2}-m_{1}}{m_{1}+m_{2}}}\right)\mathbf {u} _{2}+\left({\frac {2m_{1}}{m_{1}+m_{2}}}\right)\mathbf {u} _{1}\,.$

Birinci cismin kütlesinin diğerinkinden çok daha fazla olduğu durumda (yani, m₁ » m₂), son hızlar yaklaşık olarak şöyledir:

$\mathbf {v} _{1}=\mathbf {u} _{1}\,$

$\mathbf {v} _{2}=2\mathbf {u} _{1}-\mathbf {u} _{2}\,.$

O halde daha fazla kütleli cisim hızını değiştirmez ve daha az kütleli cisim, diğerinin hızının iki katı kadar daha hızlı ve kendi orijinal hızı kadar daha yavaş hareket eder.

Eşit kütleli iki cismin kafa-kafaya çarpışmasında (yani, m₁ = m₂), son hızlar şöyle verilir

$\mathbf {v} _{1}=\mathbf {u} _{2}\,$

$\mathbf {v} _{2}=\mathbf {u} _{1}\,.$

Yani hızlar basitçe değiş tokuş edilirler. Eğer birinci cisim sıfır olmayan u₁ ilk hızına sahip olup ikincisi ise duruyorsa, çarpışmadan sonra birinci cisim duruyor olup, ikincisi u₁ son hızı ile hareketine devam edecektir. Bu fenomenin temsili Newton beşiği ile gösterilebilir.

ÖRNEK: İlk hızları ve kütleleri: m1=1000kg, u1=5m/s, m²=0.1kg, u2=0m/s. Son hızları yaklaşık olarak verilmiştir: v1=4.999m/s, v2=9.999m/s

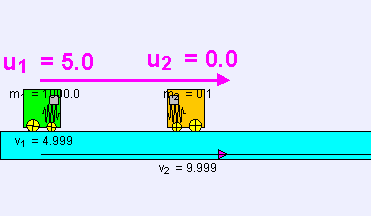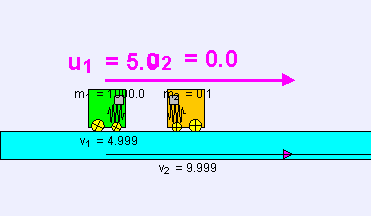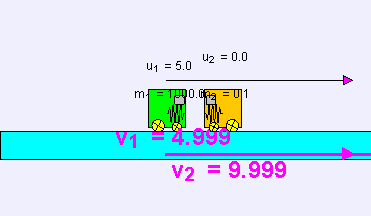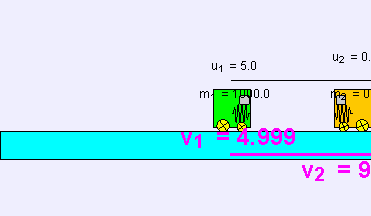
Merkezi esnek çarpışmalarda hareket doğrultusunda bir değişme olmaz. Bu çarpışmalarda kinetik enerji ve momentum korunur. Aşağıdaki iki formül merkezi esnek çarpışma problemlerinde kullanılır:

• ${\overrightarrow {P}}_{\text{1(ilk)}}+{\overrightarrow {P}}_{\text{2(ilk)}}={\overrightarrow {P}}_{\text{1(son)}}+{\overrightarrow {P}}_{\text{2(son)}}$

Çoklu boyutlarda

Birden daha üst boyutlardaki, kafa-kafaya olmayan çarpışmalardaki gibi çarpışmalarda, hız vektörü, çarpışma düzlemine dik ve çarpışma düzlemine paralel olmak üzere, iki ortogonal bileşenine ayrılır. Çarpışma düzlemine dik hız bileşenleri değişmeden kalırken, çarpışma düzlemindeki hız, bir boyutlu durumdaki gibi hesaplanabilir. Örneğin, iki-boyutlu bir çarpışmada, momenta x ve y bileşenlerine ayrıştırılabilir. Bundan sonra her bileşeni ayrı ayrı hesaplayıp, sonuçları vektörel olarak birleştirip hesaplayabiliriz. Bu vektörün büyüklüğü, kapalı sistemin son momentumudur.

Mükemmel, esnek-olmayan çarpışma

Mükemmel esnek-olmayan çarpışmaya verilen ortak bir örnek, iki kartopunun çarpışıp, akabinde birbirlerine yapışmalarıdır. Bu durumda momentumun korunumu denklemi şöyledir:

$m_{1}\mathbf {u} _{1}+m_{2}\mathbf {u} _{2}=\left(m_{1}+m_{2}\right)\mathbf {v} \,$

Mükemmel, esnek-olmayan çarpışmalar, gösterilebilir ki, kinetik enerjinin maksimum oranda diğer enerji biçimlerine dönüştüğü çarpışmalardır. Örneğin, eğer çarpışmadan sonra iki cisim yapışıp, ortak bir son hız ile hareket ediyorlarsa, daima, nesnelerin hızlarının sıfır olduğu ve böylece kinetik enerjilerinin %1,0'inin dönüştürüldüğü bir gözlem çerçevesi bulunabilir. Bu göreli durumda dahi doğru olup, parçacık hızlandırıcılarında, kinetik enerjiyi etkin bir biçimde, kütle-enerjinin değişik formlarına çevirmek için, (yani kütleli parçacıklar elde etmek için), kullanılır.

Tazmin katsayısı

Ana madde: Coefficient of Restitution

Tazmin(restitution) katsayısı, göreli uzaklaşma hızının, göreli yaklaşma hızına oranı olarak tanımlanır. Bir oran olduğundan, boyutsuz bir niceliktir. Tazmin katsayısı, iki çarpışan nesne için, şöyle verilir:

$C_{R}={\frac {v_{2}-v_{1}}{u_{1}-u_{2}}}$

burada

v₁ çarpışmadan sonra, birinci nesnenin son skaler hızı

v₂ çarpışmadan sonra, ikinci nesnenin son skaler hızı

u₁ çarpışmadan önce, birinci nesnenin ilk skaler hızı

u₂ .çarpışmadan önce, ikinci nesnenin ilk skaler hızı.

Mükemmel bir esnek çarpışma, C_R 'nin 1 olduğunu ima eder. Böylece mükemmel esnek çarpışmada, çarpışan cisimlerin göreli yaklaşma ve göreli uzaklaşma hızları eşittir.

Esnek-olmayan çarpışmalar, (C_R < 1) eşitsizliğine sahiptirler. Mükemmel bir esnek-olmayan çarpışma durumunda, çarpışan cisimlerin kütle merkezlerine göre hızları sıfırdır. Böylece cisimler, çarpışmadan sonra birbirlerine yapışırlar.

Patlamalar

Patlamalar, bir zincirleme reaksiyon sonucunda, potansiyel enerjinin kinetik enerjiye dönüşmesiyle çevrede bulunan materyallerin yer değiştirmesi şeklinde oluşurlar. Patlamalar potansiyel enerjiyi korumaz. Bunun yerine kimyasal, mekanik ya da nükleer biçimlerinde bulunan potansiyel enerjiyi, kinetik enerji, akustik enerji ve elektromagnetik ışınım biçimlerine çevirir.

Momentumun çağdaş tanımları

Göreli mekanikte momentum

Göreli mekanikte, korunabilmesi için, momentum şöyle tanımlanmalıdır

$\mathbf {p} =\gamma m_{0}\mathbf {v} \,,$

burada m₀ cismin değişmez kütle si ve ϒ

$\gamma ={\frac {1}{\sqrt {1-(v/c)^{2}}}}\,,$

İle verilen Lorentz çarpanıdır. burada v cismin hızı ve c ışık hızıdır. Tersine bağıntı şöyle verilir:

$\mathbf {v} ={\frac {c^{2}\mathbf {p} }{\sqrt {(pc)^{2}+(m_{0}c^{2})^{2}}}}={\frac {c^{2}\mathbf {p} }{E}}\,,$

Burada $p={\sqrt {p_{x}^{2}+p_{y}^{2}+p_{z}^{2}}}$ momentumun büyüklüğüdür..

Göreli momentum, değişmez kütle ile cismin has hızının çarpımı olarak da verilir. Cismin has hızı, cismin, gözlemcinin kendi gözlem çerçevesinde ölçtüğü konumunun, cismin kendi üzerinden geçen zamana göre(yani cismin has zamanına göre) olan değişim hızıdır. Klasik mekaniğin geçerli olduğu bölgede, göreli momentum, Newtonsal momentuma yakınsar: düşük hızlarda, γm₀v, yaklaşık olarak m₀v Newtonsal momentum ifadesine eşittir.

E göreli enerjisi, m₀ kütlesi, p göreli momentumu ve m = γm₀ göreli kütlesinin, grafiksel bir temsili.

Bir cismin toplam E enerjisi, göreli momentumu ile şöyle ilintilidir

$E^{2}=(pc)^{2}+(m_{0}c^{2})^{2}\,,$

burada p, p'nin büyüklüğüdür. Bu göreli enerji-momentum bağıntısı, foton gibi kütlesiz parçacıklar için bile geçerlidir; m₀ = 0 seçilirse

$E=pc\,.$

olur. Hem kütleli hem de kütlesiz parçacıklar için de, göreli momentum, de Broglie dalgaboyu λ'ya şöyle bağlıdır.

$p=h/\lambda \,,$

burada h, Planck sabitidir.

Dörtlü vektör formülasyonu

Göreli dörtlü momentum, dörtlü vektörlerin Lorentz ötelemeleri altında değişmez kalmalarından dolayı, Albert Einstein tarafından önerilmiş tir. Dörtlü-momentum P şöyle tanımlanır:

$\mathbf {P} :=(E/c,p_{x},p_{y},p_{z})\,,$

burada E = γm₀c²,sistemin toplam göreli enerjisi ve p_x, p_y ve p_z sırasıyla göreli momentumun x-, y- ve z bileşenlerini temsil eder.

Momentum dörtlü vektörünün büyüklüğü || P' ||, m₀cye eşittir, çünkü

$||\mathbf {P} ||^{2}=(E/c)^{2}-p^{2}=(m_{0}c)^{2}\,.$

dir ve her gözlem çerçevesi için değişmezdir. Kapalı bir sistemde, toplam dörtlü momentum korunur ki bu en nihayetinde hem enerjinin hem de momentumun korunumunu birleştirip, bir tek denkleme indirgemiş olur. Örneğin, in the radiationless collision of two particles with rest masses $m_{1}$ ve $m_{2}$ kütleli, $\mathbf {v} _{1}$ ve$\mathbf {v} _{2}$ ilk hızlarına sahip göreli iki parçacığın ışımasız çarpışmalarındaki, $\mathbf {v} _{3}$ ve $\mathbf {v} _{4}$ son hızları, dörtlü momentumun korunumundan aşağıdaki gibi bulunabilir

$\mathbf {P} _{1}+\mathbf {P} _{2}=\mathbf {P} _{3}+\mathbf {P} _{4}\,,$

burada

$\mathbf {P} _{i}=m_{i}\gamma _{i}(c,\mathbf {v} _{i}).$

Esnek çarpışmalarda, durgun kütle değişmez iken ($m_{1}=m_{3}$ and $m_{2}=m_{4}$), esnek olmayan çarpışmalarda durgun kütlelerde değişiklik olur. Dörtlü momentumun korunumunun, uzay-zamanın homojen olmasının bir sonucu olduğu ispatlanabilir.

Genelleştirilmiş momentum

Momentum, öteleme invaryansının Noether yüküdür. Öyle ki, sadece parçacıklar değil, alanlar ve diğer her şey momentuma sahip olabilir. Ancak uzay-zamanın eğri olduğu yerlerde, öteleme invaryansı için hiçbir Noether yükü yoktur.

Kuantum mekaniğinde momentum

Kuantum mekaniğinde, momentum, dalga fonksiyonu üzerine etkiyen bir işlemci olarak tanımlanır. Heisenberg belirsizlik ilkesi, bir sistemin aynı anda hem konumunu hem de momentumunu ne kadar hassas olarak belirleyebileceğimizin sınırların tanımlar. Kuantum mekaniğinde, konum ve momentum, eşlenik değişkenlerdir.

Konum tabanında tasvir edilen bir parçacığın momentum işlemcisi şöyledir;

$\mathbf {p} ={\hbar \over i}\nabla =-i\hbar \nabla \,,$

burada ∇ gradyen işlemcisi, ħ indirgenmiş Planck sabiti ve i sanal birimdir. Bu momentum işlemcisinin çokça kullanılan şeklidir, ancak değişik başka tabanlarda değişik biçimler alabilir. Örneğin momentum tabanında, momentum işlemcisi şöyle temsil edilir

$\mathbf {p} \psi (p)=p\psi (p)\,,$

burada ψ(p) dalga fonksiyonuna etkiyen işlemci p, dalga fonksiyonu kere p değeri sonucunu verir. Bu aynı konum işlemcisinin dalga fonksiyonuna etkidikten sonra, konum değeri x çarpı dalga fonksiyonunu vermesi gibidir.

Elektromagnetizmada momentum

Elektrik ve magnetik alanlar, durağan ya da zaman içinde değişip değişmediklerine bakılmaksızın, momentum taşırlar. Bir metal küre, silindirsel kapasitör veya mıknatıs bir çubuğun üzerindeki elektrostatik(magnetostatik) alanın P basıncı aşağıdaki gibidir.

$P_{static}={W}=\left[{\epsilon _{0}\epsilon }{\frac {{\mathbf {E} }^{2}}{2}}+{\frac {1}{\mu _{0}\mu }}{\frac {{\mathbf {B} }^{2}}{2}}\right]\,,$

burada ${W}\,$, ${\mathbf {E} }\,$, ${\mathbf {B} }\,$, Sırasıyla elektromagnetik enerji yoğunluğu, elektrik alanı ve magnetik alandır. elektromagnetik basınç, ${P}={W}\,$, kapasitörü patlatacak kadar güçlü olabilir. O halde elektrik ve magnetik alanlar da momentum taşırlar.

Işık (görülür, UV, radyo) elektromagnetik bir dalgadır ve böylece momentuma sahiptir. Fotonun kütlesi olmamasına rağmen yine de momentum taşır. Bu özellik güneş yelkeni gibi uygulamalara zemin hazırlar. Dielektrik ortamdaki ışığın momentumunun hesaplanması tartışmalıdır (Bkz Abraham–Minkowski controversy [1]3 Ocak 2012 tarihinde Wayback Machine sitesinde arşivlendi.).) Momentum, elektrodinamik bir sistemde korunur(alandaki momentumdan, hareket eden bölümlerin mekanik momentumuna dönüşebilir). Bir alanın momentumunun hesabı, genellikle enerji-momentum tensörü ve belli bir hacim üzerinden integre edilmiş Poynting vektörünün zaman içindeki değişimleri dikkate alınarak yapılır. Bu ise bileşenleri enerji yoğunluğu ve momentum yoğunluğu olan bir tensör alanıdır. Elektromagnetik etkileşmeler söz konusu olduğunda, kanonik momentuma karşılık gelen kuantum mekaniksel momentum işlemcisi

$\mathbf {p} =m\mathbf {v} \,,$

Yerine,

$\mathbf {P} =m\mathbf {v} +q\mathbf {A} \,$,

ile ifade edilir. Burada:

$\mathbf {A} \,$ elektromagnetik vektör potansiyeli

$m\,$ yüklü parçacığın kütlesi

$\mathbf {v} \,$ hızı

$q\,$ yüküdür.

Açısal momentum

Açısal momentum çember şeklinde bir düzlemde dönen bir cismin sahip olduğu bir özelliktir. Momentum gibi sabittir:

${\vec {L}}={\vec {r}}\times {\vec {p}}$

r: Parçacığın seçilen orijin noktasına göre uzaklık vektörü

p: Parçacığın momentumu

Kaynakça

• David Halliday, David (1960-2007). Fundamentals of Physics. John Wiley & Sons. Chapter 9. 
• Serway, Raymond; Jewett, John (2003). Physics for Scientists and Engineers (6 ed.). Brooks Cole. ISBN 0-534-40842-7
• Stenger, Victor J. (2000). Timeless Reality: Symmetry, Simplicity, and Multiple Universes. Prometheus Books. Chpt. 12 in particular.
• Tipler, Paul (1998). Physics for Scientists and Engineers: Vol. 1: Mechanics, Oscillations and Waves, Thermodynamics (4th ed.). W. H. Freeman. ISBN 1-57259-492-6
• Hand, Louis N.; Finch, Janet D. (1998). Analytical Mechanics. Cambridge University Press. Chapter 4. 
• Dorn Bader Physik Gymnasium Gesamtband, Sek 2, 2000 Scroedel Verlag, ISBN 3-507-10724-4
• Metzler Physik J. Grehn, J.Kause, 4. Basim, ISBN 978-3-507-10710-6