Hurwitz zeta fonksiyonu

q=1/3 olduğunda Hurwitz zeta fonksiyonu tanım kümesi renklendirmesi.

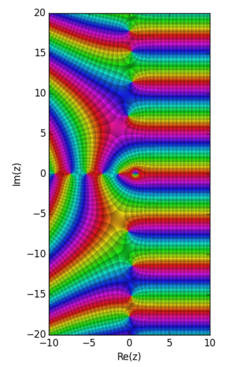
Matematik'te, Hurwitz zeta fonksiyonu, adını Adolf Hurwitz'ten almıştır, çoğunlukla zeta fonksiyonu denir. Formel tanımı için kompleks değişken s 'in Re(s)>1 ve q 'nun Re(q)>0 yardımıyla

$\zeta (s,q)=\sum _{n=0}^{\infty }{\frac {1}{(q+n)^{s}}}.$

Bu serinin tanımı verilen s ve q değerleri için mutlak yakınsaktır. Meromorf fonksiyon'a genişletilebilir. Bütün s≠1 değerleri için geçerlidir. Riemann zeta fonksiyonu için ζ(s,1)dir.

Analitik devamlılık

Hurwitz zeta fonksiyonu için analitik devamlılık genişletilirse meromorf fonksiyon olarak tanımlanır, bütün kompleks sayılar için s ile s ≠ 1. s = 1 bir basit kutup vardır. artık 1. Sabit terimlerle verilirse

$\lim _{s\to 1}\left[\zeta (s,q)-{\frac {1}{s-1}}\right]={\frac {-\Gamma '(q)}{\Gamma (q)}}=-\psi (q)$

burada Γ Gama fonksiyonu'dur ve ψ digama fonksiyonu'dur.

Seri Gösterimi

q > −1 ve herhangi kompleks s ≠ 1 için bir yakınsak seri gösterimi tanımı 1930'da Helmut Hasse tarafından verildi.

$\zeta (s,q)={\frac {1}{s-1}}\sum _{n=0}^{\infty }{\frac {1}{n+1}}\sum _{k=0}^{n}(-1)^{k}{n \choose k}(q+k)^{1-s}.$

Bu yakınsak seri s-düzleminde tam fonksiyon'un tekdüze tıkız altküme'sidir. Burada $q^{1-s}$ n inci ileri fark iç toplamı olarak görülebilir; bu şöyledir,

$\Delta ^{n}q^{1-s}=\sum _{k=0}^{n}(-1)^{n-k}{n \choose k}(q+k)^{1-s}$

Burada Δ ileri fark operatorü'dür. Böylece, yazmak istersek,

$\zeta (s,q)={\frac {1}{s-1}}\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{n+1}}\Delta ^{n}q^{1-s}$

$={\frac {1}{s-1}}{\log(1+\Delta ) \over \Delta }q^{1-s}.$

Integral Gösterimi

Bu fonksiyonun integral gösterimi Mellin dönüşümü'nün terimleri içindedir

$\zeta (s,q)={\frac {1}{\Gamma (s)}}\int _{0}^{\infty }{\frac {t^{s-1}e^{-qt}}{1-e^{-t}}}dt$

için $\Re s>1$ and $\Re q>0.$

Hurwitz formülü

Hurwitz formülü bu teoremdir:

$\zeta (1-s,x)={\frac {1}{2s}}\left[e^{-i\pi s/2}\beta (x;s)+e^{i\pi s/2}\beta (1-x;s)\right]$

burada

$\beta (x;s)=2\Gamma (s+1)\sum _{n=1}^{\infty }{\frac {\exp(2\pi inx)}{(2\pi n)^{s}}}={\frac {2\Gamma (s+1)}{(2\pi )^{s}}}{\mbox{Li}}_{s}(e^{2\pi ix})$

Bu gösterim $0\leq x\leq 1$ aralığı ve $s>1$ değerleri içindir, burada, ${\mbox{Li}}_{s}(z)$ polilogaritma'dır.

Fonksiyonel denklem

Zetanın kompleks düzlemde sağ sol yarı düzlemde fonksiyonel denklem'le ilişkili değerleri $1\leq m\leq n$ tam sayıları için

$\zeta \left(1-s,{\frac {m}{n}}\right)={\frac {2\Gamma (s)}{(2\pi n)^{s}}}\sum _{k=1}^{n}\cos \left({\frac {\pi s}{2}}-{\frac {2\pi km}{n}}\right)\;\zeta \left(s,{\frac {k}{n}}\right)$

bütün s değerleri için geçerlidir..

Taylor serisi

İkinci değişken bir zeta türevi ve bir shift(kayma)'dır:

${\frac {\partial }{\partial q}}\zeta (s,q)=-s\zeta (s+1,q).$

Böylece, Taylor serisi'nin eşik formu vardır:

$\zeta (s,x+y)=\sum _{k=0}^{\infty }{\frac {y^{k}}{k!}}{\frac {\partial ^{k}}{\partial x^{k}}}\zeta (s,x)=\sum _{k=0}^{\infty }{s+k-1 \choose s-1}(-y)^{k}\zeta (s+k,x).$

Kapalılık ilişkisi Stark-Keiper formülüdür:

$\zeta (s,N)=\sum _{k=0}^{\infty }\left[N+{\frac {s-1}{k+1}}\right]{s+k-1 \choose s-1}(-1)^{k}\zeta (s+k,N)$

tam sayı değerleri için N değişke için s tir. Bakınız Faulhaber formülü tam sayıların kuvvet serisi sonlu toplamı için benzer bir ilişki.

Fourier dönüşümü

Hurwitz zeta fonksiyonunun ayrık Fourier dönüşümü'nde skonulduğunda Legendre chi fonksiyonu olur.

Bernoulli polinomları ile ilişkisi

$\beta$ fonksiyonunun genelleştirilmiş şekli Bernoulli polinomları'dır:

$B_{n}(x)=-\Re \left[(-i)^{n}\beta (x;n)\right]$

burada $\Re z$ z reel kısmı gösterir. Karşıt olarak,

$\zeta (-n,x)=-{B_{n+1}(x) \over n+1}.$

Özel olarak, $n=0$ değeri için

$\zeta (0,x)={\frac {1}{2}}-x.$

Jacobi teta fonksiyonu ile ilişkisi

$\vartheta (z,\tau )$ fonksiyonuna Jacobi teta fonksiyonu denir, burada

$\int _{0}^{\infty }\left[\vartheta (z,it)-1\right]t^{s/2}{\frac {dt}{t}}=\pi ^{-(1-s)/2}\Gamma \left({\frac {1-s}{2}}\right)\left[\zeta (1-s,z)+\zeta (1-s,1-z)\right]$

$\Re s>0$ ise ve z kompleks ise, ama bir tam sayı değilse.. z=n tam sayısı için, bu basitçe

$\int _{0}^{\infty }\left[\vartheta (n,it)-1\right]t^{s/2}{\frac {dt}{t}}=2\ \pi ^{-(1-s)/2}\ \Gamma \left({\frac {1-s}{2}}\right)\zeta (1-s)=2\ \pi ^{-s/2}\ \Gamma \left({\frac {s}{2}}\right)\zeta (s).$

Burada ζ Riemann zeta fonksiyonu'dur. Buradaki ikinci formun fonksiyonel denklem'in orijinali Riemann tarafından verilen Riemann zeta fonksiyonu olduğu unutulmamalıdır. z ayrık tabanlı bir tam sayı olmalıdır ve burada z nin $t\rightarrow 0$ için Jacobi teta fonksiyonunun Dirac delta fonksiyonu'na yakınsaması hesaplanamaz.

Dirichlet L-fonksiyonu ile ilişkisi

Dirichlet L-fonksiyonu ile Hurwitz zeta fonksiyonu lineer kombinasyon olarak ifade edilebilir. Aynı şekilde:ζ(s) eşitlik q=1, q=1/2 ve q=n/k ve bunun yanında k>2, (n,k)>1 ise 0<n<k ise .(2^s-1)ζ(s),ya gider Hurwitz zeta fonksiyonu, Riemann zeta fonksiyonu ile çakışır ve, sonuç olarak

$\zeta (s,n/k)=\sum _{\chi }{\overline {\chi }}(n)L(s,\chi ),$

Dirichlet karakteri her zaman mod k 'dır. Ters yönde de bizim lineer kombinasyonumuz var

$L(s,\chi )={\frac {1}{k^{s}}}\sum _{n=1}^{k}\chi (n)\;\zeta \left(s,{\frac {n}{k}}\right).$

Burada çarpım teoremi

$k^{s}\zeta (s)=\sum _{n=1}^{k}\zeta \left(s,{\frac {n}{k}}\right),$

şöyle bir genelleştirme kullanılabilir

$\sum _{p=0}^{q-1}\zeta (s,a+p/q)=q^{s}\,\zeta (s,qa).$

(Bu son formda q değeri bir doğal sayıdır ve 1-qa doğal sayı değildir.)

Sıfırlar

Eğer "q" = 1 ise Hurwitz zeta fonksiyonu kendini Riemann zeta'ya indirger, q = 1 / 2 durumunda ise basit bir fonksiyonun s karmaşık argümanı çarpımı ile Riemann zeta fonksiyonuna indirgenir (s için yukarıya bakınız), her durumda Riemann zeta fonksiyonunda sıfır ile çalışmak zordur. Özellikle, burada daha gerçel kısmı 1 veya daha büyük ve hiçbir sıfır olmayacaktır. Ancak, Hurwitz's zeta fonksiyonu için 0 <q <1 ve q ≠ 1 / 2, olduğunda ise o zaman 1<Re(s)<1+ε aralığında ε gerçeldir. . Bu Davenport ve Heilbronn tarafından [2] rasyonel ve cebirsel olmayan irrasyonel q ve Cassels tarafından [3]ise cebirsel irrasyonel q için ispat edildi.

Rasyonel değerler

The Hurwitz zeta function occurs in a number of striking identities at rational values (given by Djurdje Cvijović and Jacek Klinowski, reference below). In particular, values in terms of the Euler polynomials $E_{n}(x)$:

$E_{2n-1}\left({\frac {p}{q}}\right)=(-1)^{n}{\frac {4(2n-1)!}{(2\pi q)^{2n}}}\sum _{k=1}^{q}\zeta \left(2n,{\frac {2k-1}{2q}}\right)\cos {\frac {(2k-1)\pi p}{q}}$

ve

$E_{2n}\left({\frac {p}{q}}\right)=(-1)^{n}{\frac {4(2n)!}{(2\pi q)^{2n+1}}}\sum _{k=1}^{q}\zeta \left(2n+1,{\frac {2k-1}{2q}}\right)\sin {\frac {(2k-1)\pi p}{q}}$

Bir de şu var:

$\zeta \left(s,{\frac {2p-1}{2q}}\right)=2(2q)^{s-1}\sum _{k=1}^{q}\left[C_{s}\left({\frac {k}{q}}\right)\cos \left({\frac {(2p-1)\pi k}{q}}\right)+S_{s}\left({\frac {k}{q}}\right)\sin \left({\frac {(2p-1)\pi k}{q}}\right)\right]$

$1\leq p\leq q$değeri için. Burada, $C_{\nu }(x)$ ve $S_{\nu }(x)$ ifadesiLegendre chi function anlamına gelir $\chi _{\nu }$ as

$C_{\nu }(x)=\operatorname {Re} \,\chi _{\nu }(e^{ix})$

ve

$S_{\nu }(x)=\operatorname {Im} \,\chi _{\nu }(e^{ix}).$

For integer values of ν, these may be expressed in terms of the Euler polynomials. These relations may be derived by employing the functional equation together with Hurwitz's formula, given above.

Uygulamalar

Hurwitz zeta fonksiyonu'nun birçok disiplin içinde uygulamaları vardır. En yaygın, sayı teorisi'nde ortaya çıkar ve gelişmiş derinleşmiş teoridir.. Bunun yanında, fraktal'ler ve dinamik sistemler'in derinlemesine araştırılmasında kullanılır.istatistik uygulamalarında ;Zipf's kanunu ve Zipf-Mandelbrot kanunu'nda..parçacık fiziği'nde; Julian Schwinger'in bir formülünün içindeki dirac'ın bir oranı düzgün elektrik alanındaki elektron çift üretimi için kesin sonuç verir.

Özel durumlar ve genellemeler

Hurwitz zeta fonksiyonunun genelleştirilmiş şekli poligama fonksiyonu'dur:

$\psi ^{(m)}(z)=(n-1)^{m+1}m!\zeta (m+1,z).\,$

Hurwitz zeta'nın genelleştirilmiş şekli Lerch transandant'ıdır :

$\Phi (z,s,q)=\sum _{k=0}^{\infty }{\frac {z^{k}}{(k+q)^{s}}}$

ve böylece

$\zeta (s,q)=\Phi (1,s,q).\,$

Hipergeometrik fonksiyon

$\zeta (s,a)=a^{-s}\cdot {}_{s+1}F_{s}(1,a_{1},a_{2},\ldots a_{s};a_{1}+1,a_{2}+1,\ldots a_{s}+1;1)\qquad \qquad a_{1}=a_{2}=\ldots =a_{s}=a{\text{ und }}a\notin \mathbb {N} {\text{ und }}s\in \mathbb {N} ^{+}.$

Meijer G-fonksiyon

$\zeta (s,a)=G\,_{s+1,\,s+1}^{\,1,\,s+1}\left(-1\;\left|\;{\begin{matrix}0,1-a,\ldots ,1-a\\0,-a,\ldots ,-a\end{matrix}}\right)\right.\qquad \qquad s\in \mathbb {N} ^{+}.$

Ayrıca bakınız

• Matematiksel fonksiyonların listesi

Kaynakça

• Jonathan Sondow and Eric W. Weisstein, Hurwitz Zeta Function (MathWorld)
• See chapter 12 of Şablon:Apostol IANT
• Milton Abramowitz and Irene A. Stegun, Handbook of Mathematical Functions, (1964) Dover Publications, New York. ISBN 0-486-61272-4. (See Paragraph 6.4.102 Eylül 2009 tarihinde Wayback Machine sitesinde arşivlendi. for relationship to polygamma function.)
• Djurdje Cvijović and Jacek Klinowski, "Values of the Legendre chi and Hurwitz zeta functions at rational arguments", Mathematics of Computation 68 (1999), 1623-1630.
• Victor S. Adamchik, Derivatives of the Hurwitz Zeta Function for Rational Arguments16 Mart 2010 tarihinde Wayback Machine sitesinde arşivlendi., Journal of Computational and Applied Mathematics, 100 (1998), pp 201–206.
• Linas Vepstas, The Bernoulli Operator, the Gauss-Kuzmin-Wirsing Operator, and the Riemann Zeta