Gauss fonksiyonu

μ beklenen değer ve σ² varyansına sahip normalleştirilen Gauss eğimleri. İlgili parametreler: a = 1/(σ√(2π)), b = μ, c = σ

Matematikte Gauss fonksiyonu (Fonksiyon adını Carl Friedrich Gauss'tan alır), bir fonksiyon biçimidir ve şöyle ifade edilir:

$f(x)=ae^{-{\frac {(x-b)^{2}}{2c^{2}}}}$

Bazı reel sabitler için; a, b, c ve e ≈ 2,71828...(Euler sayısı).

Gauss fonksiyonları, istatistikte normal dağılım tanımlamak için sıkça kullanılır. Ayrıca sinyal işlemede, Gauss filtresini tanımlamak; görüntü işlemede, iki boyutlu Gauss fonksiyonlarındaki Gauss bulanıklığında; matematikte, ısı denklemi ve difüzyon denklemini çözmek ve Weierstrass dönüşümünü tanımlamak için kullanılır.

Özellikleri

Normal dağılım

Gauss fonksiyonlarına üstel fonksiyon uygulanarak genel dördüncü derece fonksiyon elde edilir Gauss fonksiyonları, logaritmanın dördüncü dereceden fonksiyonlarıdır.

Gauss fonksiyonları analitiktir ve limitleri x → ∞ giderken 0'dır.

Gauss fonksiyonları ilkel fonksiyonu olmayan temel fonksiyondur. Gauss fonksiyonunun integrali hata fonksiyonudur. Tüm reel sayılardaki hata fonksiyonları, aşağıdaki Gauss integrali kullanılarak hesaplanabilir:

$\int _{-\infty }^{\infty }e^{-x^{2}}\,dx={\sqrt {\pi }}$

Bu integral aşağıdaki biçime dönüştürülebilir:

$\int _{-\infty }^{\infty }ae^{-{(x-b)^{2} \over 2c^{2}}}\,dx=ac\cdot {\sqrt {2\pi }}.$

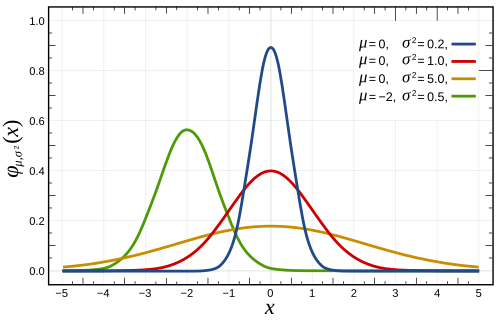
Burada, yalnızca a = 1/(c√(2π)) için integral 1'dir. Bu durumda Gauss integrali, μ = b beklenen değeri ve σ² = c² varyansına sahip normal dağıtılmış bir rassal değişkenin olasılık yoğunluk fonksiyonu olur, şöyle ki:

$g(x)={\frac {1}{\sigma {\sqrt {2\pi }}}}e^{-{\frac {1}{2}}\left({\frac {x-\mu }{\sigma }}\right)^{2}}.$

Gauss fonksiyonları Fourier dönüşümündeki belirsizlik ilkesine göre sıfıra en yakın alanda bulunurlar.

İki boyutlu Gauss fonksiyonu

2 boyutlu bir Gauss eğrisi

İki boyutta Gauss fonksiyonundaki e'nin kuvveti arttırıldığında fonksiyon dördüncü derece biçime dönüştürülür. Sonuçta Gauss fonksiyonu daima elips şeklindedir.

İki boyutlu Gauss fonksiyonuna özel bir örnek şöyle verilebilir:

$f(x,y)=A\exp \left(-\left({\frac {(x-x_{o})^{2}}{2\sigma _{x}^{2}}}+{\frac {(y-y_{o})^{2}}{2\sigma _{y}^{2}}}\right)\right).$

Burada A katsayısı genlik; x_o,y_o merkez ve σ_x, σ_y, kabarcığın x ve y yayılımlarıdır. Buradaki şekil, A = 1, x_o = 0, y_o = 0, σ_x = σ_y = 1 kullanılarak elde edildi.

Genellikle, iki boyutlu eliptik Gauss fonksiyonu şöyle ifade edilir:

$f(x,y)=A\exp \left(-\left(a(x-x_{o})^{2}+2b(x-x_{o})(y-y_{o})+c(y-y_{o})^{2}\right)\right)$

Bunun matrisi şöyledir:

$\left[{\begin{matrix}a&b\\b&c\end{matrix}}\right]$

Bu matris "pozitif tanımlı matris" olarak adlandırılır.

Bu formülasyonda A = 1, (x_o, y_o) = (0, 0), a = c = 1/2, b = 0 kullanılarak buradaki şekil elde edilir.

Genel denklem için parametrelerin anlamı

Denklemin genel biçimi için A katsayısı, tepenin yüksekliği ve (x_o, y_o), damlacığın merkezidir.

a, b ve c parametreler şöyle verilsin:

$a={\frac {\cos ^{2}\theta }{2\sigma _{x}^{2}}}+{\frac {\sin ^{2}\theta }{2\sigma _{y}^{2}}}$

$b=-{\frac {\sin 2\theta }{4\sigma _{x}^{2}}}+{\frac {\sin 2\theta }{4\sigma _{y}^{2}}}$

$c={\frac {\sin ^{2}\theta }{2\sigma _{x}^{2}}}+{\frac {\cos ^{2}\theta }{2\sigma _{y}^{2}}}$

Bu durumda damlacık saat yönünde $\theta$ açıyla döndürülür (saat yönünün tersine döndürmek için b katsayısının işaretleri yer değiştirilir). Böylece şekil şöyle olur:

$\theta =0$

$\theta =\pi /6$

$\theta =\pi /3$

Aşağıdaki Octave kodu kullanılarak parametrelerin değişim etkisi kolayca görülebilir:

A = 1;
x0 = 0; y0 = 0;

sigma_x = 1;
sigma_y = 2;

for theta = 0:pi/100:pi
a = cos(theta)^2/2/sigma_x^2 + sin(theta)^2/2/sigma_y^2;
b = -sin(2*theta)/4/sigma_x^2 + sin(2*theta)/4/sigma_y^2 ;
c = sin(theta)^2/2/sigma_x^2 + cos(theta)^2/2/sigma_y^2;

[X, Y] = meshgrid(-5:.1:5, -5:.1:5);
Z = A*exp( - (a*(X-x0).^2 + 2*b*(X-x0).*(Y-y0) + c*(Y-y0).^2)) ;
surf(X,Y,Z);shading interp;view(-36,36);axis equal;drawnow
end

Çoğu fonksiyonlar, görüntü işleme ve gözün görme sistemi fonksiyonunun modellemesini hesaplamak için sıkça kullanılır.

Çok boyutlu Gauss fonksiyonu

Ana madde: Çokdeğişirli normal dağılım

$n$ boyutlu bir uzayda Gauss fonksiyonu şöyle ifade edilir:

$f(x)=\exp(-x^{T}Ax)\;,$

Burada, $x=\{x_{1},\dots ,x_{n}\}$, $n$ koordinatlarının sütunu;, $A$, bir "pozitif tanımlı $n\times n$ matrisi" ve ${}^{T}$, matrisin transpozesini (veya devriğini) ifade eder.

Bir Gauss fonksiyonunun integrali tüm $n$ boyutlu uzayda şöyle ifade edilir:

$\int _{\mathbb {R} ^{n}}\exp(-x^{T}Bx)dx={\sqrt {\frac {\pi ^{n}}{\det {B}}}}\;.$

Biraz daha genelleştirme yapılırsa Gauss fonksiyonu şöyle olur:

$f(x)=\exp(-x^{T}Ax+s^{T}x)\;,$

Burada $s=\{s_{1},\dots ,s_{n}\}$, kaydırma vektörüdür ve $A$ matrisi $A^{T}=A$ biçiminde simetrik kabul edilebilir. Bu fonksiyona ait aşağıdaki integraller aynı yöntemle hesaplanabilir:

$\int d^{n}xe^{-x^{T}Bx+v^{T}x}={\sqrt {\frac {\pi ^{n}}{\det {B}}}}\exp({\frac {1}{4}}v^{T}B^{-1}v)\equiv {\mathcal {M}}\;.$

$\int d^{n}xe^{-x^{T}Bx+v^{T}x}\left(a^{T}x\right)=(a^{T}u)\cdot {\mathcal {M}}\;,\;{\rm {where}}\;u={\frac {1}{2}}B^{-1}v\;.$

$\int d^{n}xe^{-x^{T}Bx+v^{T}x}\left(x^{T}Dx\right)=\left(u^{T}Du+{\frac {1}{2}}{\rm {tr}}(DB^{-1})\right)\cdot {\mathcal {M}}\;.$

${\begin{aligned}&\int d^{n}xe^{-x^{T}A'x+s'^{T}x}\left(-{\frac {\partial }{\partial x}}\Lambda {\frac {\partial }{\partial x}}\right)e^{-x^{T}Ax+s^{T}x}=\\&=\left(2{\rm {tr}}(A'\Lambda AB^{-1})+4u^{T}A'\Lambda Au-2u^{T}(A'\Lambda s+A\Lambda s')+s'^{T}\Lambda s\right)\cdot {\mathcal {M}}\;,\\&{\rm {burada}}\;u={\frac {1}{2}}B^{-1}v,v=s+s',B=A+A'\;.\end{aligned}}$