Dairesel grafik

Dairesel grafik (veya dilimli diyagram, sektör grafiği) (İngilizce: "pie chart", "pasta grafiği"), istatistik biliminde betimsel istatistik alanında kategorik (ya sırasal ölçekli ya da isimsel ölçekli) verileri görsel bir şekilde betimleyip özetlemek için hazırlanan; içindeki kategori dilimlerini orantısal olarak gösteren bir daire şeklinde sunulan bir gösterim aracıdır.

Bir daire şeklindeki dairesel grafik içinde bulunan her dilim bir kategoriyi gösterir ve bu dilimin büyüklüğü derece birimi ile o kategoride bulunan veri sayısının toplam veri sayısı oranına (yani "orantılı sıklık" değerine) aynı oran ile orantılıdır. İlk defa gösterimi 1801'de İngiliz yazarı Playfair'in yayımladığı Statistical Breviary adlı bir kitapta olmuştur ve bu kitapta verilen iki dairesel grafikten birisi 1789'dan önce Osmanlı Devleti'nin değişik kitalarda olan arazilerinin coğrafî alanı verilerini özetlemektedir.^[1]

Dairesel grafik işletme alanında ve kitle iletişim dünyasında en çok kullanılan istatistik aracı olduğu kabul edilmektedir. Fakat bu aletin temellerinin iyi bilinmeden kullanılması bazı istatistikçilerin büyük tenkitlerine yol açmıştır ve bazı istatistik otoriteleri bu veri gösterim aletinin, hatalı intibalara neden olacağı için, hiç kullanılmamasını tavsiye etmişlerdir.^[2] Bunlara göre dairesel grafik kullanılmasının şu dezavantajları bulunur:

Eğer kullanılan dilim kategorileri, sırasal ölçekli veya isimsel ölçekli değil de, gruplanmış niceliksel (yani aralıksal ölçekli veya oransal ölçekli değişken verileri ise bu türlü niceliksel sayısal verileri daha açıkça ve daha kullanışlı olarak özetleyen istatistiksel grafik, (çubuk grafiği veya nokta grafiği veya histogram) veya istatistiksel tablolar (sıklık tablosu) kullanılması salık verilmektedir.
Tek bir dairesel grafiğin değişik dilimlerinin birbiriyle karşılaştırılması uygunsuzdur ve bunu uygun hale getirmek zordur.
İki değişik dairesel grafiğin birbirleriyle ikili karşılaştırılması ancak belirli sınırlayıcı şartlar bulunuyorsa uygundur ve aksi halde bu türlü ikili karşılaştırma uygun değil hatta anlamsızdır.^[3]

Fakat, bazı hallerde dairesel grafik kullanılması veri bilgilerinin açıkça anlaşılır şekilde gösterilmesi için çok etkin olabilmektedir:

Tek bir dairesel grafik dilimlerin birbirleriyle karşılaştırılmadan bu grafik içindeki tek bir dilimin tüm grafikle karşılaştırılması çok uygundur.
Eğer bu türlü karşılaştırma yapılmakta ise ve eğer ele alınan dilim tüm verilerinin %25 ile %50'si arasında ise, bu tek bir dilim ile tüm karşılaştırmasının gayet kullanışlı sonuç vereceği bildirilmiştir.^[4]

Örneğin

Bu örneğin 2004'te yapılan Avrupa Birliği Parlamento seçimleri sonucunda ortaya çıkan 8 değişik parti grubu üyelerinin sayısını gösteren bir dairesel grafiktir. Aşağıdaki tablo bu grafiğin ortaya çıkarılması için gereken hesapları göstermektedir. İlk sütun parti grubu ismini ve kısaltılmasını, ikinci sütun seçilen üye sayısını; üçüncü sütun bunların toplam üye sayısına oranlarını verir. En son sütun ise her bir parti grubu oranının, derece toplamı 360 derece olan dairede kaç derecelik dilime tekabül ettiğini gösterir ve üçüncü sütundaki her bir oranın 360 ile bölünmesi ile elde edilmiştir.

Parti Grubu	Parlamentoda üye sayısı	Orantı (%)	Dilim büyüklüğü (°)
"Avrupa Birleşik Solu-Nordik Ülkeler Yeşiller Solu (EUL)"	39	5.3	19.2
"Avrupa Sosyalistler Partisi (PES)"	200	27.3	98.4
"Avrupa Serbest Alyansı (EFA)"	42	5.7	20.7
"Demokrasiler ve Farklı Olanlar Avrupası (EDD)"	15	2.0	7.4
"Avrupa Liberal Demokrat ve Reform Partisi (ELDR)"	67	9.2	33.0
"Avrupa Halk Partisi (EPP)"	276	37.7	135.7
"Avrupa Milletleri için Birlik (UEN)"	27	3.7	13.3
Diğer	66	9.0	32.5
Toplam	732	99.9*	360.2*

*Yuvarlamalar dolayısıyla toplamlar 100 ve 360 değildir.

Bu dairesel grafikte bulunan dilimlerin derece (°) şeklinde ifade edilen büyüklüğü verinin bir kategorisinin büyüklüğünün veri sayı toplamına oranı ile orantılıdır. Büyüklüğü derece ile ifade edilen dilimlerin toplamı 360 dereceye eşit olduğu icin herhangi bir kategori için s orantılı sıklık için bu dairesel grafikteki bir dilimin derece şekilde büyüklüğü (360xs) derece olur. Örnegin, "Avrupa Halk Partisi (EPP)" için sıklık 276, orantılı sıklık (276/732=)37.7 olup dairesel grafikteki bu kategori diliminin büyüklüğü (360x37.7=)135.7 derece olur.

Kullanılımı, etkinliği ve görsel algılanması

Üç değişik veri seti için dairesel grafik ve çubuk grafiği gösterimleri.

Dairesel grafikler işletme alanında ve kitle iletişim araçlarında (özellikle dergi ve gazetelerde) çok rastlanan bir grafiktir; buna başlıca neden bu türlü grafiğin algılanması için "entelektüel züppelik" gerekmediği önyargısı olabilir. Fakat uzman istatistikçiler genel olarak dairesel grafikleri bilgilerin gösterilmesi için kalitesi düşük bir araç olduğunu kabul etmektedirler ve daha bilimsel yazılarda dairesel grafikler pek az kullanılmaktadır. Buna bir neden de psikologların değişik şekillerin algılanması üzerine yaptıkları araştırma çalışmalarına göre alanlarla ifade edilen büyüklüklerin ve büyüklüğe göre şekillerde değişmelerin yapılmasının, uzunlukla ifade edilen büyüklüklere ve bunların değişmelerine kıyasla daha zor algılandığını deneysel olarak ispat etmeleridir. Psikologlar tarafından bir psikolojik algılama ölçümü olarak kullanılan "Stevens'in güç ölçüsü"ne göre görsel alan algılama için Stevens güç endeksi 0,7 iken uzunluk algılaması için güç endeksi 1,0 olmaktadır.^[5]

ABD'de "ATT&T Bell Laboratuvarları" araştırmalarına göre, açıya göre yapılan bir karşılaştırma uzunluğa göre yapılan bir karşılaştırmadan daha zor ve daha az kesinlikle algılanmaktadır. Bu yukarıda verilen ve üç dairesel grafik ile ayni bilgiyi ihtiva eden üç çubuk grafiğini gösteren, diyagram içinde görülebilir. Bu bilgiye göre değişik dilimlerin ve değişik çubukların büyüklüğe göre sıralanması istendiğinde bu deneye katılanların büyük çoğunluğu dilimlerin büyüklüklerine göre sıralamakta güçlük çekmekte ama çubuk grafiğindeki çubukların sıralanmasını kolaylıkla yapabilmektedirler. Fakat deneyde istenen sonuç tek bir belirtilen kategori için tek bir dilimi tüm daire ile veya tek bir çubuğu toplam veri sayısı ile karşılaştırılması olursa, dairesel grafik kullanılarak çok daha çabuk doğru cevap verilmektedir. Eğer belirtilen dilimin toplama orantısı %25 ile %50 arasında ise dairesel grafik, çubuk grafiğine nazaran, çok daha etkin sonuçlara yol açmaktadır.

Değişik şekilleri ve benzer gösterimler

Florence Nightingale tarafından Kırım Harbi sırasında hazırlanan Üsküdar Selimiye Kışlası hastenesindeki ölümleri gösteren "*Doğu'daki ordudaki ölümlerin sebepleri diagramı*".

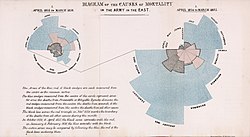
Polar alan dairesel grafik

Günümüzde "polar alan dairesel grafiği" adı verilen bir değişik dairesel grafiğinin 1858'de Florence Nightingale tarafından ilk defa kullandığı iddia edilmektedir. Flörence Nightingale'ın ünü çok açık ve çok özlü olarak verileri açıklaması dolayısıyla fikirlerini başkalarına kabul ettirebildiği bilinmektedir. Üsküdar hastanesi için çıkardığı ve bu istatistiksel aracı kullanarak gösterdiği sonuçlar ve bunların açıkça ve anlaşılır şekilde bir raporda İngiliz Kraliyet Komisyonu araştırmasına sunması onu ününün başlangıcı olmuştur.^[6]

Fakat buna benzer grafikler daha önce de kullanılmıştır. Dalgalanma olguları gösteren olayların sıklık incelemelerini ele alan bir bilimsel makalesinde 1829'da "André-Michel Guerry" "gül diyagramı" adlı benzer bir grafik kullanmıştır.^[7]

1843'te "Leon Lalanne" rüzgâr yönlerinin bir pusula yönlerine göre nasıl değiştiğini inceleyen sıklıkları bu çeşit diyagramda incelemiştir. Meteorolojiciler hala rüzgâr gülü grafiğini kullanmaktadırlar.

Polar alan grafiği alışılagelmiş olan dairesel grafiğe çok benzemektedir; ama bütün dilimler birer daire içinde aynı derecedirler ve dilim büyüklükleri her dilimin daire merkezinden ne kadar uzak olduğu ile ifade edilirler. Böylece tek bir dairede değişik kategoriler aynı açıda olan dilimler şeklinde olup dışarı taşmaları ile büyüklükleri karşılaştırılabilmektedir.

Çoklu-seviyeli dairesel grafik

"Çoklu-seviyeli dairesel grafik" bazen "köklü ağaç grafiği" olarak da bilinmekte ve birbirine bir hiyerarşi içinde bağlı olan verilerin bilgileri iç içe bir seri daireler şekilde ifade etmektedir.^[8] Merkezde bulunan daire bilgi kökünü ifade etmekte bu merkezli usuuste açılan daireler merkezden ayrılan hiyerarşileri göstermektedir. En içteki dairenin bir kesimi içinde bulunan diğer kesimler alt hiyerarşi kesimlerini gösterir.^[9]

Ayrılmış dilimli dairesel grafik

Bir dairesel grafiğe çok benzeyen ama bir veya daha fazla sayıda dilimleri birbirinden ayrılmış halde gösterilen bir grafiğe ayrılmış dilimli dairesel grafik adı verilmektedir. Bu ayrılan dilim veya dilimler sunulan grafikte bir dilim veya dilimlerin önemini vurgulamak veya geride kalan dilimlerin küçüklüğünü açıkça göstermek için kullanılmaktadır.

Üç boyutlu dairesel grafik

Bazen özellikle kütle iletişim organları bir dairesel grafiği veya bir ayrılmış dilimli dairesel grafiği sunmak için üç boyutlu gösterimler kullanıp dilimlere ve daireye bir prespektif vermektedirler. Bu üç boyutlu şekiller çok defa estetik nedenlerle kullanılmaktadır. Çok kere üç boyutlu prespektif sunulan bilgilerin daha iyice anlaşılmasına hiçbir katkı yapmamaktadır. Bazı uzmanlara göre ise, verilen üç boyutlu preskpektifini bu tip grafiklerin ve kesimlerini biçimini çarpıtıp sunulan bilgilerin anlaşılmasını zorlaştırmaktadır ve hatat yanıltıcı bilgiler edinilmesine yol açmaktadır. Uzman istatistikçiler, dairesel grafiklerde ve bütün diğer istatistiksel grafiklerde, genel olarak üç boyutlu gösterimlerin kullanılmamasını tavsiye etmektedirler.^[10]

Simit şekilli dairesel grafik

Ortası açık bir daire içindeki kesimler seklinde sunulan "simit şekilli dairesel grafik" (İngilizce "doughnut chart") bir dairesel grafikle ayni bilgiyi vermektedir. Bu grafiğin ortasında bir genişçe delik olması diğer bilgileri sağlayan diğer ayni şekilleri grafikleri arka arkaya koymaya destek vermektedir.

Tarihçe

Dairesel grafiğin ilk kullanışı 1801'de İngiliz William Playfair'in yayımladığı Statistical Breviary adlı kitapta bulunan bu türlü iki grafiktir.^[11] Bu gösterim 19. yüzyılda özel litograf tipi basım yapılmasını gerektirdiği için pek popüler olarak kullanılmamıştır. 1858'de Fransız mühendis "Charles Joseph Minard" hazırladığı haritaların bir üçüncü boyutta bilgi ihtiva etmesini isteği nedeniyle bu gösterimleri kullanması, bu gösterim usulünün yayılmasına başlangıç olmuştur.^[12]

Galeri

William Playfair'in Statistical Breviary kitabında bulunan bir dairesel grafik. 1789'dan önce Osmanlı İmparatorluğu'nun değişik kıtalarda bulunan arazi alanları.
Minard'in Fransa'nın değişik bölgelerinden et olarak tüketilmek üzere Paris'e gönderilen kocabaş hayvanların sayılarını gösteren dairesel grafik(1858).
ABD nüfusu içinde değişik ırkların dağılımı (2000) - Ayrılmış dilimli dairesel grafik.
Japonya 2005 Diet genel seçiminde partiler ve parti klikleri - Yüzük şekilde dairesel grafik.

Dipnotlar

^ Dairesel grafik ve içindeki dilimler bir İngiliz üstü yuvarlak hamurla kaplı etli veya meyveli börek gibi bir yemek olan "pie" yemeğini andırdığı için bu ilk sunumda "pie chart" ismi kullanılmıştır ve bu isim hala da kullanılmaktadır.
^ Tufte, Edward Tufte, (2001), The Visual Display of Quantitative Information. Graphics Press, ISBN 0-9613921-4-2. say. 44
^ Few, Stephen. "Save the Pies for Dessert" 16 Aralık 2010 tarihinde Wayback Machine sitesinde arşivlendi., Ağustos 2007, (İngilizce) Erişme:2.2.2010
^ Good, Phillip I. ve James W. Hardin, (2003) Common Errors in Statistics (and How to Avoid Them). Wiley. ISBN 0-471-46068-0 say.117–118 (İngilizce).
^ Bu algılama güç endeksi için bakınız: Stevens, S. S. (1957). "On the psychophysical law." Psychological Review C.64 No:3 say.153–181. PMID 13441853 (İngilizce)
^ Florence Nightingale Museum, Florence Nightingale's Statistical Diagrams [1] 4 Mart 2016 tarihinde Wayback Machine sitesinde arşivlendi. (İngilizce) (Erişim:29.10.2009)
^ Guerry, A.-M. (1829). Tableau des variations météorologique comparéeş aux phénomèneş physiologiques, d'aprés les observations faites à l'obervatoire royal, et les recherches statistique les plus récentes. Annales d'Hygiène Publique et de Médecine Légale, 1 :228-. (Fransızca)
^ 13 Mayıs 2010 tarihinde Wayback Machine sitesinde [https://web.archive.org/web/20100513031315/http://www.neoformix.com/2006/MultiLevelPieChart.html arşivlendi. Clark, Jeff (2006). Neoformix. "Multi-level Pie Charts" [2] 13 Mayıs 2010 tarihinde Wayback Machine sitesinde arşivlendi. (İngilizce) (Erişim:21.5.2010)
^ Webber Richard, Herbert Ris ve Jiangbc Wel. "Space-filling Techniques ın Visualizing Output from Computer Based Economic Models" [3] 16 Ağustos 2010 tarihinde Wayback Machine sitesinde arşivlendi. (İngilizce) (Erişim:21.5.2010)
^ Good, Phillip İ. ve Jamess W. Hardin, James (2003), Common Errors ın Statistics (and How to Avoid Them), New York:Wiley. ISBN 0-471-46068-0.
^ * Playfair, William, (2005) Commercial and Political Atlas and Statistical Breviary, Cambridge:Cambridge University Press ISBN 0-521-85554-3. (İngilizce)
^ Spence, Ian. No Humble Pie: The Origins and Uşage of a statistical Chart^{[ölü/kırık bağlantı]}. Journal of Educational and Behavioral Statistics. Kıs 2005, C.30 No.4 say. 353–368 ((ing))

Ayrıca bakınız

İstatistiksel grafik

Dış bağlantılar

Etkileşimli Java tabanlı dairesel grafik "applet"i 5 Mayıs 2015 tarihinde Wayback Machine sitesinde arşivlendi. (İngilizce) (Erişim:21.5.2010).

[1] Dairesel grafik ve içindeki dilimler bir İngiliz üstü yuvarlak hamurla kaplı etli veya meyveli börek gibi bir yemek olan "pie" yemeğini andırdığı için bu ilk sunumda "pie chart" ismi kullanılmıştır ve bu isim hala da kullanılmaktadır.

[2] Tufte, Edward Tufte, (2001), The Visual Display of Quantitative Information. Graphics Press, ISBN 0-9613921-4-2. say. 44

[3] Few, Stephen. "Save the Pies for Dessert" 16 Aralık 2010 tarihinde Wayback Machine sitesinde arşivlendi., Ağustos 2007, (İngilizce) Erişme:2.2.2010

[4] Good, Phillip I. ve James W. Hardin, (2003) Common Errors in Statistics (and How to Avoid Them). Wiley. ISBN 0-471-46068-0 say.117–118 (İngilizce).

[5] Bu algılama güç endeksi için bakınız: Stevens, S. S. (1957). "On the psychophysical law." Psychological Review C.64 No:3 say.153–181. PMID 13441853 (İngilizce)

[6] Florence Nightingale Museum, Florence Nightingale's Statistical Diagrams [1] 4 Mart 2016 tarihinde Wayback Machine sitesinde arşivlendi. (İngilizce) (Erişim:29.10.2009)

[7] Guerry, A.-M. (1829). Tableau des variations météorologique comparéeş aux phénomèneş physiologiques, d'aprés les observations faites à l'obervatoire royal, et les recherches statistique les plus récentes. Annales d'Hygiène Publique et de Médecine Légale, 1 :228-. (Fransızca)

[8] 13 Mayıs 2010 tarihinde Wayback Machine sitesinde [https://web.archive.org/web/20100513031315/http://www.neoformix.com/2006/MultiLevelPieChart.html arşivlendi. Clark, Jeff (2006). Neoformix. "Multi-level Pie Charts" [2] 13 Mayıs 2010 tarihinde Wayback Machine sitesinde arşivlendi. (İngilizce) (Erişim:21.5.2010)

[9] Webber Richard, Herbert Ris ve Jiangbc Wel. "Space-filling Techniques ın Visualizing Output from Computer Based Economic Models" [3] 16 Ağustos 2010 tarihinde Wayback Machine sitesinde arşivlendi. (İngilizce) (Erişim:21.5.2010)

[10] Good, Phillip İ. ve Jamess W. Hardin, James (2003), Common Errors ın Statistics (and How to Avoid Them), New York:Wiley. ISBN 0-471-46068-0.

[11] * Playfair, William, (2005) Commercial and Political Atlas and Statistical Breviary, Cambridge:Cambridge University Press ISBN 0-521-85554-3. (İngilizce)

[12] Spence, Ian. No Humble Pie: The Origins and Uşage of a statistical Chart^{[ölü/kırık bağlantı]}. Journal of Educational and Behavioral Statistics. Kıs 2005, C.30 No.4 say. 353–368 ((ing))

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]