Portal:Matematik

değiştirGiriş «Matematik» portaline hoş geldiniz! Matematik insanlık tarihinin en eski bilimlerinden biridir. Çok eskiden matematik, sayıların ve şekillerin bilimi olarak tanımlanırdı. Matematik de diğer bilim dalları gibi geçen zaman içinde büyük bir gelişme gösterdi. Matematik bir yönüyle resim ve müzik gibi bir sanattır. Matematikçilerin büyük çoğunluğu onu bir sanat olarak icra ederler. Matematik, başka bir yönüyle bir dildir. Galileo Galilei tabiat matematik dilinde yazılmıştır der. Devamı burada... Ana Sayfa Dizin ve Projeler Matematik Cafe değiştirGündemdeki madde İki kümenin kesişimi her iki kümede bulunan ortak öğelerden oluşur. Venn diyagramında gösterimi. Küme, "nesneler topluluğu veya yığını" olarak tanımlanan bir matematik terimi. Bu tanımdaki "nesne" soyut veya somut bir şeydir; fakat her ne olursa olsun iyi tanımlanmış olan bir şeyi, bir eşyayı ifade eder. Örneğin, "Tüm canlılar topluluğu", "Dilimiz abecesindeki harflerin topluluğu", "Masamın üzerindeki tüm kâğıtlar" tümcelerindeki nesnelerin anlaşılabilir, belirgin oldukları, kısaca iyi tanımlı oldukları açıktır. Dolayısıyla bu tümcelerin her biri bir kümeyi tarif eder. O halde, matematikte "İyi tanımlı nesnelerin bir topluluğuna küme denir" biçiminde bir tanımlama sezgisel olarak ilk başta yeterli olacaktır. Tanımda geçen nesne sözcüğü aslında yeterince açıklık ifade eden bir sözcük değildir. Ama sezgisel olarak, kümeyi oluşturan nesnelerin iyice tanımlı olduklarını; yani belirgin, başka nesnelerden ayırdedilebilir şeyler olduklarını düşünüyoruz demektir. Bir bakıma, bir kümeyi oluşturan nesnelerin tek tek neler olduklarını düşünmekten çok, bir arada düşünebilir olmaları önemsenir. Devamı... değiştirMatematik Tarihinden 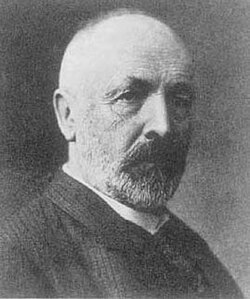Georg Ferdinand Ludwig Philipp Cantor (3 Mart 1845 – 6 Ocak 1918), Alman matematikçi. Kümeler kavramının kurucusudur. Kümeler arasında birebir eşlemenin önemini ortaya koymuş, "sonsuz küme" kavramına matematiksel bir tanım getirmiş ve gerçel sayıların sonsuzluğunun doğal sayıların sonsuzluğundan "daha büyük" olduğunu ispatlamıştır. Ayrıca kardinal sayı ve ordinal sayı kavramlarını ortaya atmış ve bu sayıların aritmetiğini tanımlamıştır. Cantor'un buluşlarının matematik ve felsefede önemli yeri vardır. Cantor'un "sonsuzötesi sayılar" fikri sezgilerimizle ters düştüğü için, zamanın matematikçileri tarafından yoğun şekilde eleştirilmiştir. Henri Poincaré, Cantor'un fikirlerini "matematiği istila eden korkunç bir hastalık" olarak nitelendirmiş, Leopold Kronecker ise Cantor'u "şarlatan"lıkla suçlamıştır. Cantor'un 1884'ten hayatının sonuna kadar yaşadığı depresyon nöbetlerinin, kısmen bu saldırılardan kaynaklandığı iddia edilmişse de, nöbetlerin asıl sebebi muhtemelen bipolar bozukluktur. Günümüzde, Cantor'un fikirleri matematikçilerin büyük çoğunluğu tarafından doğru kabul edilmekte ve matematik tarihinin en önemli paradigma değişimlerinden biri olarak tanınmaktadır. David Hilbert, "Cantor'un yarattığı cennetten bizi kimse kovamayacaktır" diyerek Cantor'un katkılarının önemini vurgulamıştır. Devamı... değiştirBunları Biliyor Muydunuz Harezmi'nin Hesab-ül Cebir vel-Mukabele adlı kitabının, matematik tarihinde, birinci ve ikinci dereceden denklemlerin sistematik çözümlerinin yer aldığı ilk eser olduğunu biliyor muydunuz? değiştirGündemdeki Resim 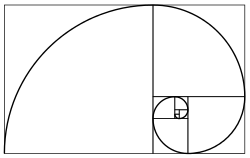"bir Fibonacci spirali ardışık Fibonacci karelerinin dairesel karşı köşe bağlantılarının çizimiyle oluşturulabilir; bunun için kullanılan kare boyutları 1, 1, 2, 3, 5, 8, 13, 21, ve 34. bkz Altın oran." değiştirHaftanın Maddesi Üstel fonksiyon ez, N sonsuza giderken (1 + z/N)N'nin limitine eşittir. Böylece, eiπ ifadesi (1 + iπ/N)N'nin limitine eşit olur. Bu canlandırmada N, 1'den 100'e kadar değişen değerler almaktadır. (1 + iπ/N)N ifadesinin hesaplanması karmaşık düzlemde gerçekleştirilen N çarpımın bütüncül etkisiyle açıklanır. N arttıkça (1 + iπ/N)N ifadesinin limiti -1'e yakınsar. Euler özdeşliği, Matematiksel çözümlemede mucidinin adıyla adlandırılan ve Leonhard Euler tarafından bulunan eşitlik $e^{i\pi }+1=0,\,\!$ dır. Burada, $e\,\!$, doğal logaritma tabanı Euler sayısını, $i\,\!$, karesi -1'e eşit olan karmaşık sayıyı, $\pi \,\!$, bir çemberin çevre uzunluğunun çapına oranına eşit olan pi sayısını ifade eder. Euler özdeşliği zaman zaman Euler denklemi olarak da adlandırılmaktadır. Devamı... değiştirSözler “ Dünyadaki en mâsum uğraş matematiktir ~ - Godfrey Harold Hardy ” Matematik Sözleri değiştirSeçkin ve Kaliteli içerik Seçkin maddeler Seçkin listeler Kaliteli maddeler Seçkin resimler Seçkin portaller Carl Friedrich Gauss Rubik Küpü 1 − 2 + 3 − 4 + · · · Sonsuz maymun teoremi Bernt Michael Holmboe Henri Brocard Rubik Küpü değiştirMatematiğin dalları Genel Temelleri Sayılar teorisi Ayrık matematik Matematikçiler Matematik tarihi Matematiğin felsefesi Matematiksel işaretler Matematiğin şiirselliği Matematik eğitimi Matematiğin dalları Basit matematik konularının listesi Matematiksel sembollerin listesi Popüler matematik Matematiğin zaman çizelgesi Matematik yarışmaları listesi Matematik ödülleri listesi Matematiğin temelleri Matematiksel mantık İspat teorisi Gödel'in eksiklik teoremi Model teorisi Özyineleme teorisi Küme teorisi (portal) Naif küme teorisi Aksiyomsal küme teorisi Kategori teorisi (portal) Topoz teorisi Sayılar teorisi (portal) Cebirsel sayılar teorisi Analitik sayılar teorisi Aritmetik Aritmetiğin temel teoremi Sayılar Doğal sayılar Asal sayılar Rasyonel sayılar Cebirsel sayılar Ayrık matematik (portal) Kombinatorikler Kombinetoriksel geometri Kodlama teorisi Kombinetoriksel tasarım Graf teorisi Sıra teorisi Kafes teorisi Cebir Analiz Geometri ve topoloji Uygulamalı matematik Cebir (portal) Temel cebir Soyut cebir Grup teorisi Halka teorisi Cisim kuramı Değişmeli cebir Geometrik cebir Lineer cebir Matris teorisi Çoklu lineer cebir Evrensel cebir Cebirin temel teoremi Analiz (portal) Hesap Hesabın temel teoremi Vektör hesabı Geometrik hesap Ölçü teorisi Reel analiz Karmaşık analiz Diferansiyel denklemler Adi diferansiyel denklemler Kısmi diferansiyel denklemler İntegral denklemler Yaklaşım teorisi Özel fonksiyonlar Potansiyel teori Harmonik analiz Fourier analizi Fonksiyonel analiz Operatör teorisi Geometri (portal) Öklid geometrisi Trigonometri Analitik geometri Öklitsel-olmayan geometri Afin geometri İzdüşüm geometrisi Dışbükey geometri Ayrık geometri Cebirsel geometri Diferansiyel geometri Riemann geometrisi Lie grupları Topoloji (portal) Genel topoloji Cebirsel topoloji Geometrik topoloji Diferansiyel topoloji Uygulamalı matematik Matematiksel modelleme Matematiksel fizik Dinamik sistemler Kontrol teorisi Değişkenlerin hesabı Matematiksel ekonomi Oyun teorisi Matematiksel finans İstatistik (portal) Olasılık teorisi Stokastik süreçler Nümerik analiz Teorik bilgisayar bilimi Kriptoloji (portal) Bilgi kuramı değiştirİlgili Portaller Fizik Astronomi

---

Portal nedir? | Portal listesi | Portal dizini | Portal kategorileri
Seçkin portaller | Sayfayı yenile